4.2 Directed Graphs
Digraphs.
A directed graph (or digraph) is a set of vertices and a collection of directed edges that each connects an ordered pair of vertices. We say that a directed edge points from the first vertex in the pair and points to the second vertex in the pair. We use the names 0 through V-1 for the vertices in a V-vertex graph.
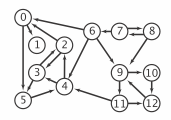
Glossary.
Here are some definitions that we use.- A self-loop is an edge that connects a vertex to itself.
- Two edges are parallel if they connect the same ordered pair of vertices.
- The outdegree of a vertex is the number of edges pointing from it.
- The indegree of a vertex is the number of edges pointing to it.
- A subgraph is a subset of a digraph's edges (and associated vertices) that constitutes a digraph.
- A directed path in a digraph is a sequence of vertices in which there is a (directed) edge pointing from each vertex in the sequence to its successor in the sequence, with no repeated edges.
- A directed path is simple if it has no repeated vertices.
- A directed cycle is a directed path (with at least one edge) whose first and last vertices are the same.
- A directed cycle is simple if it has no repeated vertices (other than the requisite repetition of the first and last vertices).
- The length of a path or a cycle is its number of edges.
- We say that a vertex w is reachable from a vertex v if there exists a directed path from v to w.
- We say that two vertices v and w are strongly connected if they are mutually reachable: there is a directed path from v to w and a directed path from w to v.
- A digraph is strongly connected if there is a directed path from every vertex to every other vertex.
- A digraph that is not strongly connected consists of a set of strongly connected components, which are maximal strongly connected subgraphs.
- A directed acyclic graph (or DAG) is a digraph with no directed cycles.

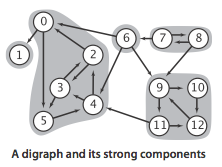
Digraph graph data type.
We implement the following digraph API.

The key method adj() allows client code to iterate through the vertices adjacent from a given vertex.
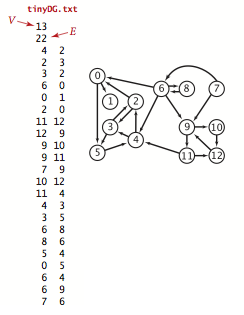
We prepare the test data tinyDG.txt using the following input file format.
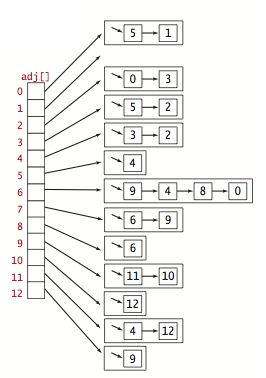
Graph representation.
We use the adjacency-lists representation, where we maintain a vertex-indexed array of lists of the vertices connected by an edge to each vertex.
Digraph.java implements the digraph API using the adjacency-lists representation. AdjMatrixDigraph.java implements the same API using the adjacency-matrix representation.
Reachability in digraphs.
Depth-first search and breadth-first search are fundamentally digraph-processing algorithms.- Single-source reachability: Given a digraph and source s, is there a directed path from s to v? If so, find such a path. DirectedDFS.java uses depth-first search to solve this problem.
- Multiple-source reachability: Given a digraph and a set of source vertices, is there a directed path from any vertex in the set to v? DirectedDFS.java uses depth-first search to solve this problem.
- Single-source directed paths: given a digraph and source s, is there a directed path from s to v? If so, find such a path. DepthFirstDirectedPaths.java uses depth-first search to solve this problem.
- Single-source shortest directed paths: given a digraph and source s, is there a directed path from s to v? If so, find a shortest such path. BreadthFirstDirectedPaths.java uses breadth-first search to solve this problem.
Cycles and DAGs.
Directed cycles are of particular importance in applications that involve processing digraphs. The input file tinyDAG.txt corresponds to the following DAG:
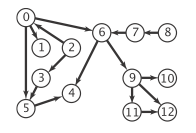
- Directed cycle detection: does a given digraph have a directed cycle? If so, find such a cycle. DirectedCycle.java solves this problem using depth-first search.
- Depth-first orders:
Depth-first search search visits each vertex exactly once.
Three vertex orderings are of interest in typical applications:
- Preorder: Put the vertex on a queue before the recursive calls.
- Postorder: Put the vertex on a queue after the recursive calls.
- Reverse postorder: Put the vertex on a stack after the recursive calls.
DepthFirstOrder.java computes these orders.

- Topological sort: given a digraph, put the vertices in order
such that all its directed edges point from a vertex earlier in the order to a
vertex later in the order (or report that doing so is not possible).
Topological.java solves this problem
using depth-first search. Remarkably, a reverse postorder in a DAG provides
a topological order.

Proposition.
A digraph has a topological order if and only if it is a DAG.Proposition.
Reverse postorder in a DAG is a topological sort.Proposition.
With depth-first search, we can topologically sort a DAG in time proportional to V + E.Strong connectivity.
Strong connectivity is an equivalence relation on the set of vertices:- Reflexive: Every vertex v is strongly connected to itself.
- Symmetric: If v is strongly connected to w, then w is strongly connected to v.
- Transitive: If v is strongly connected to w and w is strongly connected to x, then v is also strongly connected to x.

Remarkably, KosarajuSharirSCC.java implements the API with just a few lines of code added to CC.java, as follows:
- Given a digraph G, use DepthFirstOrder.java to compute the reverse postorder of its reverse, GR.
- Run standard DFS on G, but consider the unmarked vertices in the order just computed instead of the standard numerical order.
- All vertices reached on a call to the recursive dfs() from the constructor are in a strong component (!), so identify them as in CC.
Proposition.
The Kosaraju-Sharir algorithm uses preprocessing time and space proportional to V + E to support constant-time strong connectivity queries in a digraph.Transitive closure.
The transitive closure of a digraph G is another digraph with the same set of vertices, but with an edge from v to w if and only if w is reachable from v in G.
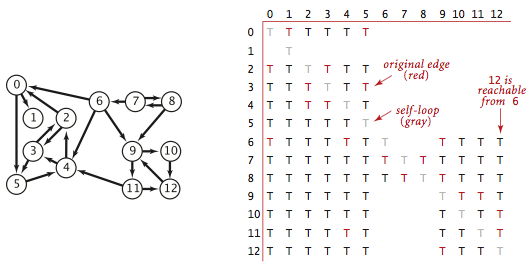
TransitiveClosure.java computes the
transitive closure of a digraph by running depth-first search
from each vertex and storing the results.
This solution is ideal for small or dense digraphs,
but it is not a solution for the large digraphs we might encounter
in practice because the constructor uses space proportional to V^2
and time proportional to V (V + E).
Exercises
- Create a copy constructor for Digraph that takes as input a digraph G and creates and initializes a new copy of the digraph. Any changes a client makes to G should not affect the newly created digraph.
-
How many strong components are there in the digraph on p. 591?
Solution: 10. The input file is mediumDG.txt.
- What are the strong components of a DAG?
- True or false: The reverse postorder of a digraph's reverse is the same as the postorder of the digraph.
-
True or false: If we modify the Kosaraju-Sharir algorithm to run the first
depth-first search in the digraph G
(instead of the reverse digraph G^R) and the second depth-first search
in G^R (instead of G), then it will still find the strong components.
Solution. True, the strong components of a digraph are the same as the strong components of its reverse.
- True or false: If we modify the Kosaraju-Sharir algorithm to replace the second depth-first search with breadth-first search, then it will still find the strong components.
-
Compute the memory usage of a Digraph with V
vertices and E edges, under the memory cost model of Section 1.4.
Solution. 56 + 40V + 64E. MemoryOfDigraph.java computes it empirically assuming that no Integer values are cached—Java typically caches the integers -128 to 127.
Creative Problems
-
Directed Eulerian cycle.
A directed Eulerian cycle is a directed cycle that contains each
edge exactly once. Write a digraph client
DirectedEulerianCycle.java
that find a directed Eulerian cycle or reports that no such cycle exists.
Hint: Prove that a digraph G has a directed Eulerian cycle if and only if vertex in G has its indegree equal to its outdegree and all vertices with nonzero degree belong to the same strong component.
-
Strong component.
Describe a linear-time algorithm for computing the strong component
containing a given vertex v. On the basis of that algorithm, describe
a simple quadratic-time algorithm for computing the strong components of a
digraph.
Partial solution: To compute the strong component containing s
- Find the set of vertices reachable from s
- Find the set of vertices that can reach s
- Take the intersection of the two sets
-
Hamiltonian path in DAGs.
Given a DAG, design a linear-time algorithm to determine whether
there is a directed path that visits each vertex exactly once.
Solution: Compute a topological sort and check if there is an edge between each consecutive pair of vertices in the topological order.
-
Unique topological ordering.
Design an algorithm to determine whether a digraph has a
unique topological ordering.
Hint: a digraph has a unique topological ordering if and only if there is a directed edge between each pair of consecutive vertices in the topological order (i.e., the digraph has a Hamiltonian path). If the digraph has multiple topological orderings, then a second topological order can be obtained by swapping a pair of consecutive vertices.
-
2-satisfiability.
Given a boolean formula in conjunctive normal form with M clauses
and N literals such that each clause has exactly two literals,
find a satisfying assignment (if one exists).
Solution sketch: Form the implication digraph with 2N vertices (one per literal and its negation). For each clause x + y, include edges from y' to x and from x' to y. Claim: The formula is satisfiable if and only if no variable x is in the same strong component as its negation x'. Moreover, a topological sort of the kernel DAG (contract each strong component to a single vertex) yields a satisfying assignment.
-
Queue-based topological order algorithm.
Develop a nonrecursive topological sort implementation
TopologicalX.java
that maintains a vertex-indexed array that keeps
track of the indegree of each vertex.
Initialize the array and a queue of sources in a single pass
through all the edges, as in Exercise 4.2.7.
Then, perform the following operations until the source queue is empty:
- Remove a source from the queue and label it.
- Decrement the entries in the indegree array corresponding to the destination vertex of each of the removed vertex's edges.
- If decrementing any entry causes it to become 0, insert the corresponding vertex onto the source queue.
-
Shortest directed cycle.
Given a digraph, design an algorithm to find a directed cycle with
the minimum number of edges (or report that the graph is acyclic).
The running time of your algorithm should be proportional to E V
in the worst case.
Application: give a set of patients in need of kidney transplants, where each patient has a family member willing to donate a kidney, but of the wrong type. Willing to donate to another person provided their family member gets a kidney. Then hospital performs a "domino surgery" where all transplants are done simultaneously.
Solution: run BFS from each vertex s. The shortest cycle through s is an edge v->s, plus a shortest path from s to v. ShortestDirectedCycle.java.
-
Odd-length directed cycle.
Design a linear-time algorithm to determine whether a digraph has an odd-length
directed cycle.
Solution. We claim that a digraph G has an odd-length directed cycle if and only if one (or more) of its strong components is nonbipartite (when treated as an undirected graph).
- If the digraph G has an odd-length directed cycle, then this cycle will be entirely contained in one of the strong components. When the strong component is treated as an undirected graph, the odd-length directed cycle becomes an odd-length cycle. Recall that an undirected graph is bipartite if and only if it has no odd-length cycle.
- Suppose a strong component of G is nonbipartite (when treated as an undirected graph). This means that there is an odd-length cycle C in the strong component, ignoring direction. If C is a directed cycle, then we are done. Otherwise, if an edge v->w is pointing in the "wrong" direction, we can replace it with an odd-length path that is pointing in the opposite direction (which preserves the parity of the number of edges in the cycle). To see how, note that there exists a directed path P from w to v because v and w are in the same strong component. If P has odd length, then we replace edge v->w by P; if P has even length, then this path P combined with v->w is an odd-length cycle.
-
Reachable vertex in a DAG.
Design a linear-time algorithm to determine whether a DAG has a vertex
that is reachable from every other vertex.
Solution. Compute the outdegree of each vertex. If the DAG has exactly one vertex v with outdegree 0, then it is reachable from every other vertex.
-
Reachable vertex in a digraph.
Design a linear-time algorithm to determine whether a digraph has a vertex
that is reachable from every other vertex.
Solution. Compute the strong components and kernel DAG. Apply Exercise 4.2.37 to the kernel DAG.
- Web crawler. Write a program WebCrawler.java that uses breadth-first search to crawl the web digraph, starting from a given web page. Do not explicitly build the web digraph.
Web Exercises
- Symbol digraph. Modify SymbolGraph.java to create a program SymbolDigraph.java that implements a symbol digraph.
- Combinational circuits. Determining the truth value of a combinational circuit given its inputs is a graph reachability problem (on a directed acyclic graph).
- Privilege escalation. Include an array from user class A to user class B if A can gain the privileges of B. Find all users that can obtain Administrator access in Windows.
- Unix program tsort.
- Checkers. Extend the rules of checkers to an N-by-N checkerboard. Show how to determine whether a checker can become in king in the current move. (Use BFS or DFS.) Show how to determine whether black has a winning move. (Find a directed Eulerian path.)
- Preferential attachment model. Web has a scale-free property and obeys a power law. New pages tend to preferentially attach to popular pages. Start with a single page that points to itself. At each step a new page appears with outdegree 1. With probability p the page points to a random page; with probability (1-p) the page points to an existing page with probability proportional to the indegree of the page.
- Subtype checking. Given single inheritance relations (a tree), check if v is an ancestor of w. Hint: v is an ancestor of w if and only if pre[v] <= pre[w] and post[v] >= post[w].
- Subtype checking. Repeat previous question, but with a DAG instead of a tree.
- LCA of a rooted tree.
Given a rooted tree and two vertices v and w, find the
lowest common ancestor (lca) of v and w.
The lca of v and w is the shared ancestor furthest from
the root.
Among most fundamental problem on rooted trees.
Possible to solve in O(1) time per query with linear
preprocessing time (Harel-Tarjan,
Bender-Coloton).
Find a DAG where the shortest ancestral path goes to a common ancestor x that is not an LCA.
- Nine-letter word.
Find a nine-letter English word such that remains an English word
after successively removing each of its letters (in an appropriate
order). Build a digraph with words and vertices and an
edge from one word to another if it can be formed by adding
one letter.
Answer: one solution is startling -> starting -> staring -> string -> sting -> sing -> sin -> in -> i.
- Spreadsheet recalculate. Hopefully no cyclic dependencies. Use topological sort of formula cell graph to determine in which order to update the cells.
- Nesting boxes.
A d-dimensional box with dimensions (a1, a2, ..., ad) nests inside
a box with dimensions (b1, b2, ..., bd) if the coordinates of the second box
can be permuted so that a1 < b1, a2 < b2, ..., ad < bd.
- Give an efficient algorithm for determining where one d-dimensional box nests inside another. Hint: sort.
- Show that nesting is transitive: if box i nests inside box j and box j nests inside box k, then box i nests inside box k.
- Given a set of n d-dimensional boxes, given an efficient algorithm to find the most boxes that can be simultaneously nested.
Hint: Create a digraph with an edge from box i to box j if box i nests inside box j. Then run topological sort.
- Warshall's transitive closure algorithm. WarshallTC.java algorithm is ideal for dense graphs. Relies on AdjMatrixDigraph.java.
- Brute-force strong components algorithm. BruteSCC.java computes the strong components by first computing the transitive closure. It takes O(EV) time and O(V^2) space.
- Tarjan's strong components algorithm. TarjanSCC.java implements Tarjan's algorithm for computing strong components.
- Gabow's strong components algorithm. GabowSCC.java implements Gabow's algorithm for computing strong components.
- Digraph generator. DigraphGenerator.java generated various digraphs.
- Finite Markov chains.
Recurrent state: once started in state, Markov chain will return with probability 1.
Transient state: some probability that it will never return
(some node j for which i can reach j, but j can't reach i).
Irreducible Markov chain = all states recurrent.
A Markov chain is irreducible if and only if it is strongly connected.
The recurrent components are those with no leave edges in the kernel DAG.
Communicating classes in Markov chain are the strong components.
Theorem. If G is strongly connected, then there is a unique stationary distribution pi. Moreover pi(v) > 0 for all v.
Theorem. If the kernel DAG of G has a single supernode with no leaving edges, then there is a unique stationary distribution pi. Moreover pi(v) > 0 for all v recurrent and pi(v) = 0 for all v transient.
- Descendants lemma. [R. E. Tarjan]
Denote by pre[v] and post[v] as the preorder and postorder number of v, respectively,
and by nd[v] the number of descendants of v (including v).
Prove that the following four conditions are equivalent.
- Vertex v is an ancestor of vertex w.
- pre[v] <= pre[w] < pre[v] + nd(v).
- post[v] - nd [v] < post[w] <= post[v]
- pre[v] <= pre[w] and post[v] >= post[w] (nesting lemma)
- Edge lemma. [R. E. Tarjan]
Prove that an edge (v, w) is one of the following four kinds:
- w is a child of v: (v, w) is a tree edge.
- w is a descendant but not a child of v: (v, w) is a forward edge.
- w is an ancestor of v: (v, w) is a back edge
- w and v are unrelated and pre[v] > pre[w]: (v, w) is a cross edge.
- Path lemma. [R. E. Tarjan] Prove that any path from v to w with pre[v] < pre[w] contains a common ancestor of v and w.
- Prove that if (v, w) is an edge and pre[v] < pre[w], then v is an ancestor of w in the DFS tree.
- Postorder lemma. [R. E. Tarjan]
Prove that if P is a path such that the last vertex x is highest in postorder,
then every vertex on the path is a descendant of x (and hence has a path from x).
Solution. The proof is by induction on the length of P (or by contradiction). Let (v, w) be an edge such that w is a descendant of x and post[v] < post[x]. Since w is a descendant of x, we have pre[w] >= pre[x].
- If pre[v] >= pre[x], then v is a descendant of x (by the nesting lemma).
- If pre[v] < pre[x], then pre[v] < pre[w], which implies (by the previous exercise) that v is an ancestor of w and hence related to x. But post[v] < post[x] implies v is a descendant of x.
- Pre-topological order.
Design a linear-time algorithm to find a pre-topological order:
and ordering of the vertices such that
if there is a path from v to w and w appears before v in the ordering,
then there must also be a path from w to v.
Hint: reverse postorder is a pre-topological order. This is the crux of the proof of correctness of the Kosaraju-Sharir algorithm.
- Wordnet. Using WordNet to Measure Semantic Orientations of Adjectives.
- Garbage collection.
Automatic memory management in languages like Java is a
challenging problem. Allocating memory is easy, but discovering
when a program is finished with memory (and reclaiming it)
is more difficult.
Reference counting: doesn't work with circular linked structure.
Mark-and-sweep algorithm. Root = local variables and static variables.
Run DFS from roots, marking all variables references from roots,
and so on.
Then, make second pass: free all unmarked objects and unmark
all marked objects. Or a copying garbage collector would then move all of the
marked objects to a single memory area.
Uses one extra bit per object.
JVM must pause while garbage collection occurs. Fragments memory.
Applications: C leak detector (leak = unreachable, unfreed memory).
- Directed cycle detection applications. Application: check for illegal inheritance loop, check for deadlocking. A directory is a list of files and other directories. A symbolic link is a reference to another directory. When listing all files in a directory, need to be careful to avoid following a cycle of symbolic links!
- Topological sort applications. Application: course prerequisites, order in which to compile components of a large computer program, causalities, class inheritance, deadlocking detection, temporal dependencies, pipeline of computing jobs, check for symbol link loop, evaluate formula in spreadsheet.
- Strong component applications. Applications to CAD, Markov chains (irreducible), spider traps and web search, pointer analysis, garbage collection.
- One-way street theorem. Implement an algorithm to orient the edges in an undirected graph so that it is strongly connected. Robbins theorem asserts that this is possible if and only if the undirected graph is two-edge connected (no bridges). In this case, a solution is to run DFS and oriented all edges in the DFS tree away from the root and all of the remaining edges toward the root.
- Orient edges in mixed graph to make acyclic.
A mixed graph is a graph with some edges that are directed and others that
are undirected. Design a linear-time algorithm to determine whether it
is possible to orient the undirected edges so that the resulting digraph
is acyclic.
Application: old city with narrow roads wants to make every road one way but still allow every intersection in the city to be reachable from every other city.
- Orient edges in mixed graph to make a directed cycle.
A mixed graph is a graph with some edges that are directed and others that
are undirected. Design a linear-time algorithm to determine whether it
is possible to orient the undirected edges so that the resulting digraph
has a directed cycle.
Application: determining whether a maximum flow is unique.
Solution: one algorithm.
- Postorder lemma variant. Let S and T be two strong components in a digraph G. Prove that if there is an edge e from a vertex in S to a vertex in T, then the highest postorder number of a vertex in S is higher than the higher postorder number of a vertex in T.
- Number of paths in a DAG.
Given a DAG and two distinguished vertices s and t,
design a linear-time algorithm to compute the number of directed paths
from s to t.
Hint: topological sort.
- Path of length L in a DAG. Given a DAG and two distinguished vertices s and t, design an algorithm to determine if there exists a path from s to t containing exactly L edges.
- Core vertices.
Given a digraph G, a vertex v is a core vertex if every vertex in G is reachable from v.
Design a linear-time algorithm that finds all core vertices.
Hint: create the strong components of G and look at the kernel DAG.
- Strong components and bipartite matching.
Given a bipartite graph G, an unmatched edge
is one that does not appear in any
perfect matching. Design an algorithm to find all unmatched edges.
Hint: prove that the following algorithm does the job. Find a perfect matching in G; orient the edges in the matching from one side of the bipartition to the other side; orient the remaining edges in the opposite direction; among the edges not in the perfect matching, return those that have endpoints in different strongly connected components.
- Transitive reduction of a digraph. The transitive reduction of a digraph is a digraph with the fewest number of edges that has the same transitive closure as the original digraph. Design an V (E + V) algorithm to compute the transitive reduction of a digraph. Note that the transitive reduction in a digraph is not necessarily unique and may not be a subgraph of the original digraph. (The transitive reduction in a DAG is unique and is a subgraph of the original digraph.)
- Odd-length path.
Given a digraph G and a source vertex s, design a linear-time algorithm
to determine all vertices that are reachable from s via a path (not necessarily
simple) with an odd number of edges.
Solution. Create a new digraph G' with two vertices v and v' for each vertex v in G. For each edge v->w in G, include two edges: v->w' and w->v'. Now, any path from s to v' in G' corresponds to an odd-length path from s to v in G. Run either BFS or DFS to determine the vertices reachable from s.
- Find a topological order of a DAG that cannot be computed as the reverse postorder of a DFS, no matter in which order the DFS chooses starting vertices in the constructor. Show that every topological order of a DAG can be computed as the reverse postorder of a DFS, provided that the DFS can choose the order of the starting vertices in the constructor arbitrarily.
- Nonrecursive DFS. Write a program NonrecursiveDirectedDFS.java that implements depth-first search using an explicit stack instead of recursion. Write a program NonrecursiveDirectedCycle.java that find a directed cycle without using recursion.
- Nonrecursive topological sort. Extend the queue-based topological sort algorithm TopologicalX.java from Exercise 4.2.39 to find a directed cycle if the digraph has a directed cycle. Name your program DirectedCycle.java.
- Cartalk puzzle. Find the longest word in a dictionary that has the property that you can remove one letter at a time (from either end or the middle) and the resulting string is also a word in the dictionary. For example, STRING is a 6-letter word with this property (STRING -> STING -> SING -> SIN -> IN -> I).
- Reverse postorder vs. preorder. True or false: The reverse postorder of a digraph is the same as the preorder of the digraph.
- Reverse postorder vs. preorder in Kosaraju–Sharir.
Suppose that you use the preorder of the digraph instead of the reverse postorder in the
Kosaraju–Sharir algorithm. Will it still produce the strong components?
Answer: No, run KosarajuSharirPreorderSCC.java on tinyDG.txt.


