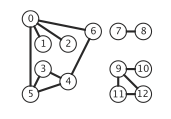
4.1 Undirected Graphs

Graphs.

A graph is a set of vertices and a collection of edges that each connect a pair of vertices. We use the names 0 through V-1 for the vertices in a V-vertex graph.

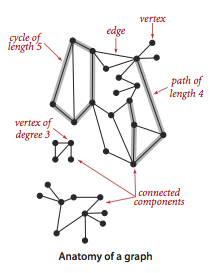
Glossary.

Here are some definitions that we use.

A self-loop is an edge that connects a vertex to itself.
Two edges are parallel if they connect the same pair of vertices.
When an edge connects two vertices, we say that the vertices are adjacent to one another and that the edge is incident on both vertices.
The degree of a vertex is the number of edges incident on it.
A subgraph is a subset of a graph's edges (and associated vertices) that constitutes a graph.
A path in a graph is a sequence of vertices connected by edges, with no repeated edges.
A simple path is a path with no repeated vertices.
A cycle is a path (with at least one edge) whose first and last vertices are the same.
A simple cycle is a cycle with no repeated vertices (other than the requisite repetition of the first and last vertices).
The length of a path or a cycle is its number of edges.
We say that one vertex is connected to another if there exists a path that contains both of them.
A graph is connected if there is a path from every vertex to every other vertex.
A graph that is not connected consists of a set of connected components, which are maximal connected subgraphs.
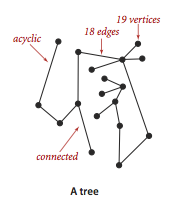
An acyclic graph is a graph with no cycles.
A tree is an acyclic connected graph.
A forest is a disjoint set of trees.
A spanning tree of a connected graph is a subgraph that contains all of that graph's vertices and is a single tree. A spanning forest of a graph is the union of the spanning trees of its connected components.
A bipartite graph is a graph whose vertices we can divide into two sets such that all edges connect a vertex in one set with a vertex in the other set.

Undirected graph data type.

We implement the following undirected graph API.

The key method adj() allows client code to iterate through the vertices adjacent to a given vertex. Remarkably, we can build all of the algorithms that we consider in this section on the basic abstraction embodied in adj().

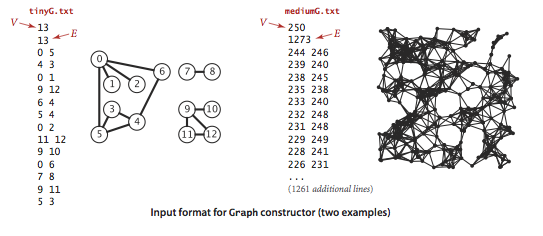
We prepare the test data tinyG.txt, mediumG.txt, and largeG.txt, using the following input file format.

GraphClient.java contains typical graph-processing code.

Graph representation.

We use the adjacency-lists representation, where we maintain a vertex-indexed array of lists of the vertices connected by an edge to each vertex.

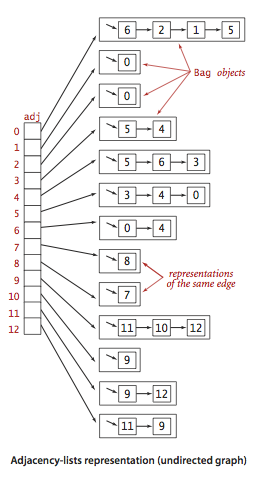
Adjacency-lists
representation of an undirected graph

Graph.java implements the graph API using the adjacency-lists representation. AdjMatrixGraph.java implements the same API using the adjacency-matrix representation.

Depth-first search.

Depth-first search is a classic recursive method for systematically examining each of the vertices and edges in a graph. To visit a vertex

Mark it as having been visited.
Visit (recursively) all the vertices that are adjacent to it and that have not yet been marked.

DepthFirstSearch.java implements this approach and the following API:

Finding paths.

It is easy to modify depth-first search to not only determine whether there exists a path between two given vertices but to find such a path (if one exists). We seek to implement the following API:

To accomplish this, we remember the edge v-w that takes us to each vertex w for the first time by setting edgeTo[w] to v. In other words, v-w is the last edge on the known path from s to w. The result of the search is a tree rooted at the source; edgeTo[] is a parent-link representation of that tree. DepthFirstPaths.java implements this approach.

Breadth-first search.

Depth-first search finds some path from a source vertex s to a target vertex v. We are often interested in finding the shortest such path (one with a minimal number of edges). Breadth-first search is a classic method based on this goal. To find a shortest path from s to v, we start at s and check for v among all the vertices that we can reach by following one edge, then we check for v among all the vertices that we can reach from s by following two edges, and so forth.

To implement this strategy, we maintain a queue of all vertices that have been marked but whose adjacency lists have not been checked. We put the source vertex on the queue, then perform the following steps until the queue is empty:

Remove the next vertex v from the queue.
Put onto the queue all unmarked vertices that are adjacent to v and mark them.

BreadthFirstPaths.java is an implementation of the Paths API that finds shortest paths. It relies on Queue.java for the FIFO queue.

Connected components.

Our next direct application of depth-first search is to find the connected components of a graph. Recall from Section 1.5 that "is connected to" is an equivalence relation that divides the vertices into equivalence classes (the connected components). For this task, we define the following API:

CC.java uses DFS to implement this API.

Proposition. DFS marks all the vertices connected to a given source in time proportional to the sum of their degrees and provides clients with a path from a given source to any marked vertex in time proportional to its length.

Proposition. For any vertex v reachable from s, BFS computes a shortest path from s to v (no path from s to v has fewer edges). BFS takes time proportional to V + E in the worst case.

Proposition. DFS uses preprocessing time and space proportional to V + E to support constant-time connectivity queries in a graph.

More depth-first search applications.

The problems that we have solved with DFS are fundamental. Depth-first search can also be used to solve the following problems:

Cycle detection: Is a given graph acyclic? Cycle.java uses depth-first search to determine whether a graph has a cycle, and if so return one. It takes time proportional to V + E in the worst case.
Two-colorability: Can the vertices of a given graph be assigned one of two colors in such a way that no edge connects vertices of the same color? Bipartite.java uses depth-first search to determine whether a graph has a bipartition; if so, return one; if not, return an odd-length cycle. It takes time proportional to V + E in the worst case.
Bridge: A bridge (or cut-edge) is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. Bridge.java uses depth-first search to find time the bridges in a graph. It takes time proportional to V + E in the worst case.
Biconnectivity: An articulation vertex (or cut vertex) is a vertex whose removal increases the number of connected components. A graph is biconnected if it has no articulation vertices. Biconnected.java uses depth-first search to find the bridges and articulation vertices. It takes time proportional to V + E in the worst case.
Planarity: A graph is planar if it can be drawn in the plane such that no edges cross one another. The Hopcroft-Tarjan algorithm is an advanced application of depth-first search that determines whether a graph is planar in linear time.

Symbol graphs.

Typical applications involve processing graphs using strings, not integer indices, to define and refer to vertices. To accommodate such applications, we define an input format with the following properties:

Vertex names are strings.
A specified delimiter separates vertex names (to allow for the possibility of spaces in names).
Each line represents a set of edges, connecting the first vertex name on the line to each of the other vertices named on the line.

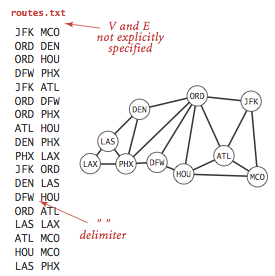
The input file routes.txt is a small example.

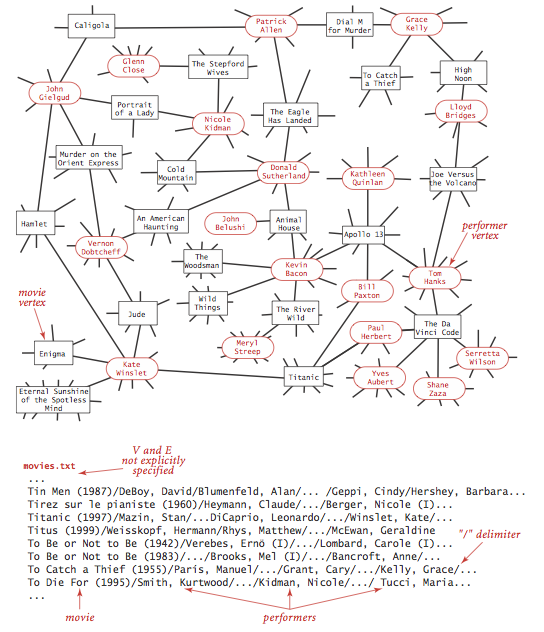
The input file movies.txt is a larger example from the Internet Movie Database. This file consists of lines listing a movie name followed by a list of the performers in the movie.

API. The following API allows us to use our graph-processing routines for such input files.
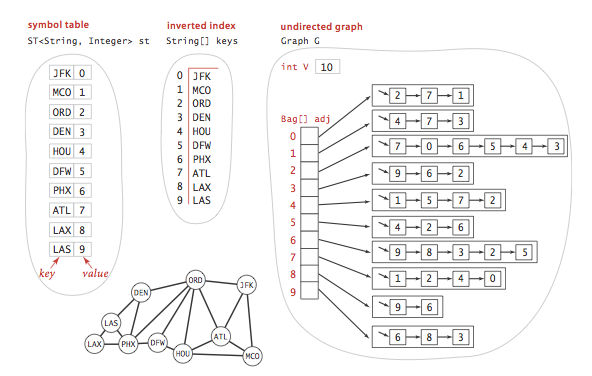
Implementation. SymbolGraph.java implements the API. It builds three data structures:
- A symbol table st with String keys (vertex names) and int values (indices)
- An array keys[] that serves as an inverted index, giving the vertex name associated with each integer index
- A Graph G built using the indices to refer to vertices
Degrees of separation. DegreesOfSeparation.java uses breadth-first search to find the degree of separation between two individuals in a social network. For the actor-movie graph, it plays the Kevin Bacon game.

Exercises

Create a copy constructor for Graph.java that takes as input a graph G and creates and initializes a new copy of the graph. Any changes a client makes to G should not affect the newly created graph.
Add a distTo() method to BreadthFirstPaths.java, which returns the number of edges on the shortest path from the source to a given vertex. A distTo() query should run in constant time.
Write a program BaconHistogram.java that prints a histogram of Kevin Bacon numbers, indicating how many performers from movies.txt have a Bacon number of 0, 1, 2, 3, ... . Include a category for those who have an infinite number (not connected to Kevin Bacon).
Write a SymbolGraph client DegreesOfSeparationDFS.java that uses depth-first instead of breadth-first search to find paths connecting two performers.
Determine the amount of memory used by Graph to represent a graph with V vertices and E edges, using the memory-cost model of Section 1.4.
Solution. 56 + 40V + 128E. MemoryOfGraph.java computes it empirically assuming that no Integer values are cached—Java typically caches the integers -128 to 127.

Creative Problems

Parallel edge detection. Devise a linear-time algorithm to count the parallel edges in a graph.
Hint: maintain a boolean array of the neighbors of a vertex, and reuse this array by only reinitializing the entries as needed.
Two-edge connectivity. A bridge in a graph is an edge that, if removed, would separate a connected graph into two disjoint subgraphs. A graph that has no bridges is said to be two-edge connected. Develop a DFS-based data type Bridge.java for determining whether a given graph is edge connected.

Web Exercises

Find some interesting graphs. Are they directed or undirected? Sparse or dense?
Degree. The degree of a vertex is the number of incident edges. Add a method int degree(int v) to Graph that returns the degree of the vertex v.
Suppose you use a stack instead of a queue when running breadth-first search. Does it still compute shortest paths?
DFS with an explicit stack. Give an example of possibility of stack overflow with DFS using the function call stack, e.g., line graph. Modify DepthFirstPaths.java so that it uses an explicit stack instead of the function call stack.
Perfect maze. Generate a perfect maze like this one

Write a program Maze.java that takes a command-line argument n, and generates a random n-by-n perfect maze. A maze is perfect if it has exactly one path between every pair of points in the maze, i.e., no inaccessible locations, no cycles, and no open spaces. Here's a nice algorithm to generate such mazes. Consider an n-by-n grid of cells, each of which initially has a wall between it and its four neighboring cells. For each cell (x, y), maintain a variable north[x][y] that is true if there is wall separating (x, y) and (x, y + 1). We have analogous variables east[x][y], south[x][y], and west[x][y] for the corresponding walls. Note that if there is a wall to the north of (x, y) then north[x][y] = south[x][y+1] = true. Construct the maze by knocking down some of the walls as follows:
1. Start at the lower level cell (1, 1).
2. Find a neighbor at random that you haven't yet been to.
3. If you find one, move there, knocking down the wall. If you don't find one, go back to the previous cell.
4. Repeat steps ii. and iii. until you've been to every cell in the grid.
Hint: maintain an (n+2)-by-(n+2) grid of cells to avoid tedious special cases.
Here is a Mincecraft maze created by Carl Eklof using this algorithm.

Getting out of the maze. Given an n-by-n maze (like the one created in the previous exercise), write a program to find a path from the start cell (1, 1) to the finish cell (n, n), if it exists. To find a solution to the maze, run the following algorithm, starting from (1, 1) and stopping if we reach cell (n, n).

explore(x, y)
-------------
  - Mark the current cell (x, y) as "visited."
  - If no wall to north and unvisited, then explore(x, y+1).
  - If no wall to east and  unvisited, then explore(x+1, y).
  - If no wall to south and unvisited, then explore(x, y-1).
  - If no wall to west and  unvisited, then explore(x-1, y).

Maze game. Develop a maze game like this one from gamesolo.com, where you traverse a maze, collecting prizes.
Actor graph. An alternate (and perhaps more natural) way to compute Kevin Bacon numbers is to build a graph where each node is an actor. Two actors are connected by an edge if they appear in a movie together. Calculate Kevin Bacon numbers by running BFS on the actor graph. Compare the running time versus the algorithm described in the text. Explain why the approach in the text is preferable. Answer: it avoids multiple parallel edges. As a result, it's faster and uses less memory. Moreover, it's more convenient since you don't have to label the edges with the movie names - all names get stored in the vertices.
Center of the Hollywood universe. We can measure how good of a center that Kevin Bacon is by computing their Hollywood number. The Hollywood number of Kevin Bacon is the average Bacon number of all the actors. The Hollywood number of another actor is computed the same way, but we make them be the source instead of Kevin Bacon. Compute Kevin Bacon's Hollywood number and find an actor and actress with better Hollywood numbers.
Fringe of the Hollywood universe. Find the actor (who is connected to Kevin Bacon) that has the highest Hollywood number.
Word ladders. Write a program WordLadder.java that takes two 5 letter strings from the command line, and reads in a list of 5 letter words from standard input, and prints out a shortest word ladder connecting the two strings (if it exists). Two words can be connected in a word ladder chain if they differ in exactly one letter. As an example, the following word ladder connects green and brown.
green greet great groat groan grown brown
You can also try out your program on this list of 6 letter words.
Faster word ladders. To speed things up (if the word list is very large), don't write a nested loop to try all pairs of words to see if they are adjacent. To handle 5 letter words, first sort the word list. Words that only differ in their last letter will appear consecutively in the sorted list. Sort 4 more times, but cyclically shift the letters one position to the right so that words that differ in the ith letter will appear consecutively in one of the sorted lists.
Try out this approach using a larger word list with words of different sizes. Two words of different lengths are neighbors if the smaller word is the same as the bigger word, minus the last letter, e.g., brow and brown.
Suppose you delete all of the bridges in an undirected graph. Are the connected components of the resulting graph the biconnected components? Answer: no, two biconnected components can be connected through an articulation point.
Bridges and articulation points.
A bridge (or cut edge) is an edge whose removal disconnects the graph. An articulation point (or cut vertex) is a vertex whose removal (and removal of all incident edges) disconnects the remaining graph. Bridges and articulations points are important because they represent a single point of failure in a network. Brute force: delete edge (or vertex) and check connectivity. Takes O(E(V + E)) and O(V(V + E)) time, respectively. Can improve both to O(E + V) using clever extension to DFS.
Biconnected components. An undirected graph is biconnected if for every pair of vertices v and w, there are two vertex-disjoint paths between v and w. (Or equivalently a simple cycle through any two vertices.) We define a cocyclicity equivalence relation on the edges: two edges e1 and e2 are are in same biconnected component if e1 = e2 or there exists a cycle containing both e1 and e2. Two biconnected components share at most one vertex in common. A vertex is an articulation point if and only if it is common to more than one biconnected component. Program Biconnected.java identifies the bridges and articulation points.
Biconnected components. Modify Biconnected to print out the edges that constitute each biconnected component. Hint: each bridge is its own biconnected component; to compute the other biconnected components, mark each articulation point as visited, and then run DFS, keeping track of the edges discovered from each DFS start point.
Perform numerical experiments on the number of connected components for random undirected graphs. Phase change around 1/2 V ln V. (See Property 18.13 in Algs Java.)
Rogue. (Andrew Appel.) A monster and a player are each located at a distinct vertex in an undirected graph. In the role playing game Rogue, the player and the monster alternate turns. In each turn the player can move to an adjacent vertex or stays put. Determine all vertices that the player can reach before the monster. Assume the player gets the first move.
Rogue. (Andrew Appel.) A monster and a player are each located at a distinct vertex in an undirected graph. The goal of the monster is to land on the same vertex as the player. Devise an optimal strategy for the monster.
Articulation point. Let G be a connected, undirected graph. Consider a DFS tree for G. Prove that vertex v is an articulation point of G if and only if either (i) v is the root of the DFS tree and has more than one child or (ii) v is not the root of the DFS tree and for some child w of v there is no back edge between any descendant of w (including w) and a proper ancestor of v. In other words, v is an articulation point if and only if (i) v is the root and has more than one child or (ii) v has a child w such that low[w] >= pre[v].
Sierpinski gasket. Nice example of an Eulerian graph.
Preferential attachment graphs. Create a random graph on V vertices and E edges as follows: start with V vertices v1, .., vn in any order. Pick an element of sequence uniformly at random and add to end of sequence. Repeat 2E times (using growing list of vertices). Pair up the last 2E vertices to form the graph.
Roughly speaking, it's equivalent to adding each edge one-by-one with probability proportional to the product of the degrees of the two endpoints. Reference.
Wiener index. The Wiener index of a vertex is the sum of the shortest path distances between v and all other vertices. The Wiener index of a graph G is the sum of the shortest path distances over all pairs of vertices. Used by mathematical chemists (vertices = atoms, edges = bonds).
Random walk. Easy algorithm for getting out of a maze (or st connectivity in a graph): at each step, take a step in a random direction. With complete graph, takes V log V time (coupon collector); for line graph or cycle, takes V^2 time (gambler's ruin). In general the cover time is at most 2E(V-1), a classic result of Aleliunas, Karp, Lipton, Lovasz, and Rackoff.
Deletion order. Given a connected graph, determine an order to delete the vertices such that each deletion leaves the (remaining) graph connected. Your algorithm should take time proportional to V + E in the worst case.
Center of a tree. Given a graph that is a tree (connected and acyclic), find a vertex such that its maximum distance from any other vertex is minimized.
Hint: find the diameter of the tree (the longest path between two vertices) and return a vertex in the middle.
Diameter of a tree. Given a graph that is a tree (connected and acyclic), find the longest path, i.e., a pair of vertices v and w that are as far apart as possible. Your algorithm should run in linear time.
Hint. Pick any vertex v. Compute the shortest path from v to every other vertex. Let w be the vertex with the largest shortest path distance. Compute the shortest path from w to every other vertex. Let x be the vertex with the largest shortest path distance. The path from w to x gives the diameter.
Bridges with union-find. Let T be a spanning tree of a connected graph G. Each non-tree edge e in G forms a fundamental cycle consisting of the edge e plus the unique path in the tree joining its endpoings. Show that an edge is a bridge if and only if it is not on some fundamental cycle. Thus, all bridges are edges of the spanning tree. Design an algorithm to find all of the bridges (and bridge components) using E + V time plus E + V union-find operations.

Nonrecursive depth-first search. Write a program NonrecursiveDFS.java that implements depth-first search with an explicit stack instead of recursion.

Here is an alternate implementation suggested by Bin Jiang in the early 1990s. The only extra memory is for a stack of vertices but that stack must support arbitrary deletion (or at least the movement of an arbitrary item to the top of the stack).

private void dfs(Graph G, int s) {
    SuperStack<Integer> stack = new SuperStack<Integer>();
    stack.push(s);
    while (!stack.isEmpty()) {
        int v = stack.peek();
        if (!marked[v]) {
            marked[v] = true;
            for (int w : G.adj(v)) {
                if (!marked[w]) {
                    if (stack.contains(w)) stack.delete(w);
                    stack.push(w);
                }
            }
        }
        else {
            // v's adjacency list is exhausted
            stack.pop();
        }
    }
}

Here is yet another implementation. It is, perhaps, the simplest nonrecursive implementation, but it uses space proportional to E + V in the worst case (because more than one copy of a vertex can be on the stack) and it explores the vertices adjacent to v in the reverse order of the standard recursive DFS. Also, an edgeTo[v] entry may be updated more than once, so it may not be suitable for backtracking applications.

private void dfs(Graph G, int s) {
    Stack<Integer> stack = new Stack<Integer>();
    stack.push(s);
    while (!stack.isEmpty()) {
        int v = stack.pop();
        if (!marked[v]) {
            marked[v] = true;
            for (int w : G.adj(v)) {
                if (!marked[w]) {
                    edgeTo[w] = v;
                    stack.push(w);
                 }
            }
        }
    }
}

Nonrecursive depth-first search. Explan why the following nonrecursive method (analogous to BFS but using a stack instead of a queue) does not implement depth-first search.

private void dfs(Graph G, int s) {
    Stack<Integer> stack = new Stack<Integer>();
    stack.push(s);
    marked[s] = true;
    while (!stack.isEmpty()) {
       int v = stack.pop();
       for (int w : G.adj(v)) {
           if (!marked[w]) {
               stack.push(w);
               marked[w] = true;
               edgeTo[w] = v;
           }
       }
    }
}

Solution: Consider the graph consisting of the edges 0-1, 0-2, 1-2, and 2-1, with vertex 0 as the source.

Matlab connected components. bwlabel() or bwlabeln() in Matlab label the connected components in a 2D or kD binary image. bwconncomp() is newer version.
Shortest path in complement graph. Given a graph G, design an algorithm to find the shortest path (number of edges) between s and every other vertex in the complement graph G'. The complement graph contains the same vertices as G but includes an edge v-w if and only if the edge v-w is not in G. Can you do any better than explicitly computing the complement graph G' and running BFS in G'?
Delete a vertex without disconnecting a graph. Given a connected graph, design a linear-time algorithm to find a vertex whose removal (deleting the vertex and all incident edges) does not disconnect the graph.
Hint 1 (using DFS): run DFS from some vertex s and consider the first vertex in DFS that finishes.
Hint 2 (using BFS): run BFS from some vertex s and consider any vertex with the highest distance.
Spanning tree. Design an algorithm that computes a spanning tree of a connected graph is time proportional to V + E. Hint: use either BFS or DFS.
All paths in a graph. Write a program AllPaths.java that enumerates all simple paths in a graph between two specified vertices. Hint: use DFS and backtracking. Warning: there many be exponentially many simple paths in a graph, so no algorithm can run efficiently for large graphs.