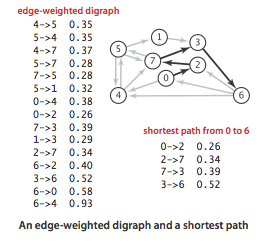
4.4 Shortest Paths

Shortest paths.

An edge-weighted digraph is a digraph where we associate weights or costs with each edge. A shortest path from vertex s to vertex t is a directed path from s to t with the property that no other such path has a lower weight.

Properties.

We summarize several important properties and assumptions.

Paths are directed. A shortest path must respect the direction of its edges.
The weights are not necessarily distances. Geometric intuition can be helpful, but the edge weights weights might represent time or cost.
Not all vertices need be reachable. If t is not reachable from s, there is no path at all, and therefore there is no shortest path from s to t.
Negative weights introduce complications. For the moment, we assume that edge weights are positive (or zero).
Shortest paths are normally simple. Our algorithms ignore zero-weight edges that form cycles, so that the shortest paths they find have no cycles.
Shortest paths are not necessarily unique. There may be multiple paths of the lowest weight from one vertex to another; we are content to find any one of them.
Parallel edges and self-loops may be present. In the text, we assume that parallel edges are not present and use the notation v->w to refer to the edge from v to w, but our code handles them without difficulty.

Edge-weighted digraph data type.

We represent the weighted edges using the following API:

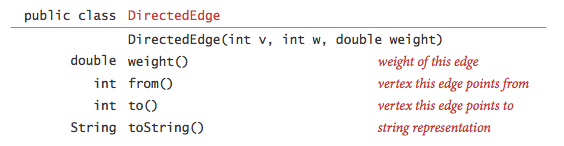
The from() and to() methods are useful for accessing the edge's vertices. DirectedEdge.java implements this API.

We represent edge-weighted digraphs using the following API:

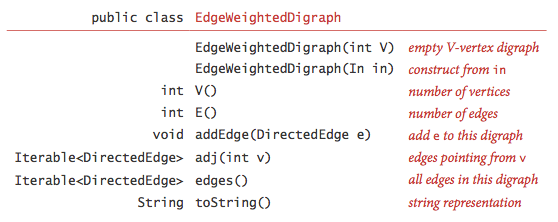
EdgeWeightedDigraph.java implements the API using the adjacency-lists representation.

Shortest paths API.

We use the following API for computing the shortest paths of an edge-weighted digraph:

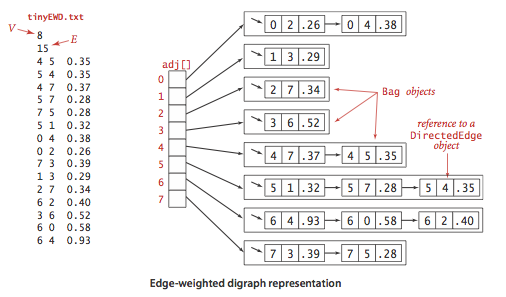
We prepare some test data:

tinyEWD.txt contains 8 vertices and 15 edges
mediumEWD.txt contains 250 vertices and 2,546 edges
1000EWG.txt contains 1,000 vertices and 16,866 edges
10000EWG.txt contains 10,000 vertices and 123,462 edges
largeEWG.txt contains one million vertices and 15,172,126 edges.

Data structures for single-source shortest paths.

Given an edge-weighted digraph and a designated vertex s, a shortest-paths tree (SPT) is a subgraph containing s and all the vertices reachable from s that forms a directed tree rooted at s such that every tree path is a shortest path in the digraph.

We represent the shortest paths with two vertex-indexed arrays:

Edges on the shortest-paths tree: edgeTo[v] is the the last edge on a shortest path from s to v.
Distance to the source: distTo[v] is the length of the shortest path from s to v.

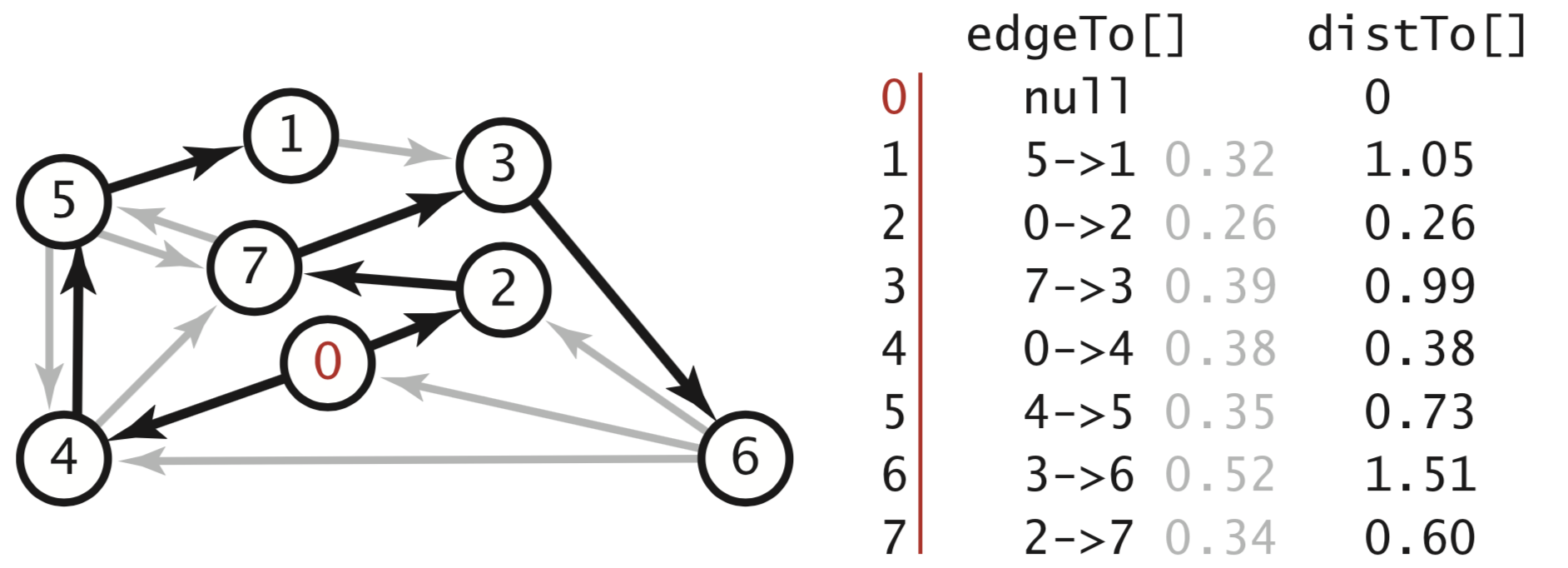
Relaxation.

Our shortest-paths implementations are based on an operation known as relaxation. We initialize distTo[s] to 0 and distTo[v] to infinity for all other vertices v.

Edge relaxation. To relax an edge v->w means to test whether the best known way from s to w is to go from s to v, then take the edge from v to w, and, if so, update our data structures.

private void relax(DirectedEdge e) {
    int v = e.from(), w = e.to();
    if (distTo[w] > distTo[v] + e.weight()) {
        distTo[w] = distTo[v] + e.weight();
        edgeTo[w] = e;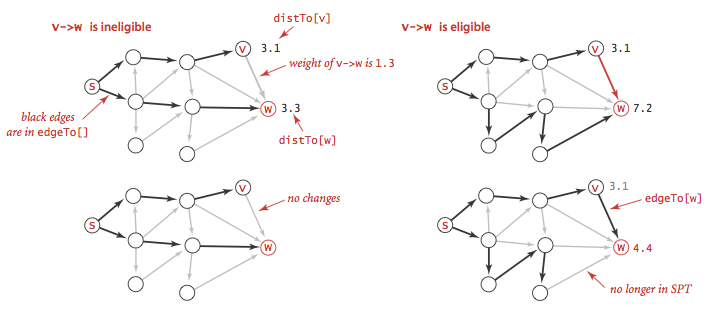
    }
}

Vertex relaxation. All of our implementations actually relax all the edges pointing from a given vertex.

private void relax(EdgeWeightedDigraph G, int v) {
    for (DirectedEdge e : G.adj(v)) {
        int w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
        }
    }
}

Dijkstra's algorithm.

Dijkstra's algorithm initializing dist[s] to 0 and all other distTo[] entries to positive infinity. Then, it repeatedly relaxes and adds to the tree a non-tree vertex with the lowest distTo[] value, continuing until all vertices are on the tree or no non-tree vertex has a finite distTo[] value.

DijkstraSP.java is an efficient implementation of Dijkstra's algorithm. It uses IndexMinPQ.java for the priority queue.

Proposition.

Dijkstra's algorithm solves the single-source shortest-paths problem in edge-weighted digraphs with nonnegative weights using extra space proportional to V and time proportional to E log V (in the worst case).

Acyclic edge-weighted digraphs.

We use the term edge-weighted DAG to refer to an acyclic edge-weighted digraph.

Single-source shortest paths problem in edge-weighted DAGs. We now consider an algorithm for finding shortest paths that is simpler and faster than Dijkstra's algorithm for edge-weighted DAGs.
- It solves the single-source problem in linear time.
- It handles negative edge weights.
- It solves related problems, such as finding longest paths.
The algorithm combines vertex relaxation with topological sorting. We initialize distTo[s] to 0 and all other distTo[] values to infinity, then relax the vertices, one by one, taking the vertices in topological order. AcyclicSP.java is an implementation of this approach. It relies on this version of Topological.java, extended to support edge-weighted digraphs.
Single-source longest paths problem in edge-weighted DAGs. We can solve the single-source longest paths problems in edge-weighted DAGs by initializing the distTo[] values to negative infinity and switching the sense of the inequality in relax(). AcyclicLP.java implements this approach.
Critical path method. We consider the parallel precedence-constrained job scheduling problem: Given a set of jobs of specified duration to be completed, with precedence constraints that specify that certain jobs have to be completed before certain other jobs are begun, how can we schedule the jobs on identical processors (as many as needed) such that they are all completed in the minimum amount of time while still respecting the constraints?

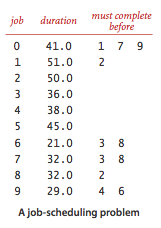
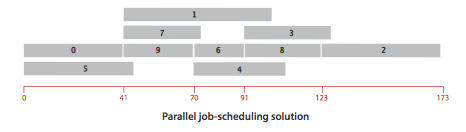
This problem can be solved by formulating it as a longest paths problem in an edge-weighted DAG: Create an edge-weighted DAG with a source s, a sink t, and two vertices for each job (a start vertex and an end vertex). For each job, add an edge from its start vertex to its end vertex with weight equal to its duration. For each precedence constraint v->w, add a zero-weight edge from the end vertex corresponding to v to the beginning vertex corresponding to w. Also add zero-weight edges from the source to each job's start vertex and from each job's end vertex to the sink.

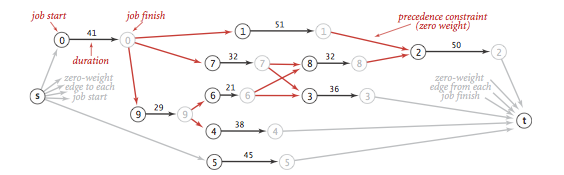
Now, schedule each job at the time given by the length of its longest path from the source.

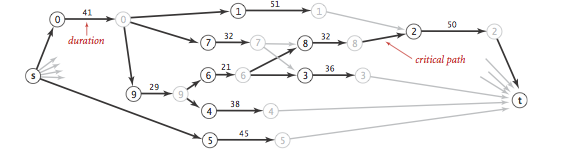
CPM.java is an implementation of the critical path method.

Proposition.

By relaxing vertices in topological order, we can solve the single-source shortest-paths and longest-paths problems for edge-weighted DAGs in time proportional to E + V.

Shortest paths in general edge-weighted digraphs.

We can solve shortest path problems if (i) all weights are nonnegative or (ii) there are no cycles.

Negative cycles. A negative cycle is a directed cycle whose total weight (sum of the weights of its edges) is negative. The concept of a shortest path is meaningless if there is a negative cycle.

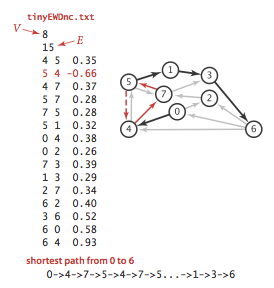
Accordingly, we consider edge-weighted digraphs with no negative cycles.
Bellman-Ford algorithm. Initialize distTo[s] to 0 and all other distTo[] values to infinity. Then, considering the digraph's edges in any order, and relax all edges. Make V such passes.
for (int pass = 0; pass < G.V(); pass++) for (int v = 0; v < G.V(); v++) for (DirectedEdge e : G.adj(v)) relax(e);
We do not consider this version in detail because it always relaxes V E edges.
Queue-based Bellman-Ford algorithm. The only edges that could lead to a change in distTo[] are those leaving a vertex whose distTo[] value changed in the previous pass. To keep track of such vertices, we use a FIFO queue. BellmanFordSP.java implements this approach by maintaining two additional data structures:
- A queue of vertices to be relaxed
- A vertex-index boolean array onQ[] that indicates which vertices are on the queue, to avoid duplicates
Negative cycle detection. In many applications, our goal is to check for and to check for and extract negative cycles. Accordingly, we add the following methods to the API:

There is a negative cycle reachable from the source if and only if the queue is nonempty after the Vth pass through all the edges. Moreover, the subgraph of edges in our edgeTo[] array must contain a negative cycle. Accordingly, to implement negativeCycle() BellmanFordSP.java builds an edge-weighted digraph from the edges in edgeTo[] and looks for a cycle in that digraph. To find the cycle, it uses EdgeWeightedDirectedCycle.java, a version of DirectedCycle.java from Section 4.3, adapted to work for edge-weighted digraphs. We amortize the cost of this check by performing this check only after every Vth edge relaxation.
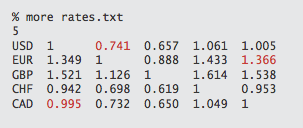
Arbitrage detection. Consider a market for financial transactions that is based on trading commodities. The table in rates.txt shows conversion rates among currencies. The first line in the file is the number V of currencies; then the file has one line per currency, giving its name followed by the conversion rates to the other currencies. An arbitrage opportunity is a directed cycle such that the product of the exchange rates is greater than one. For example, our table says that 1,000 U.S. dollars will buy 1,000.00 × .741 = 741 euros, then we can buy 741 × 1.366 = 1,012.206 Canadian dollars with our euros, and finally, 1,012.206 × .995 = 1,007.14497 U.S. dollars with our Canadian dollars, a 7.14497-dollar profit!

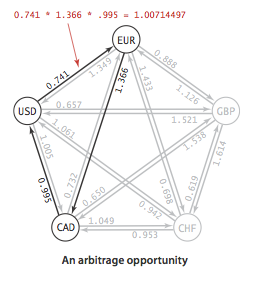
To formulate the arbitrage problem as a negative-cycle detection problem, replace each weight by its logarithm, negated. With this change, computing path weights by multiplying edge weights in the original problem corresponds to adding them in the transformed problem. Arbitrage.java identifies arbitrage opportunities in a currency-exchange network by solving the corresponding negative cycle detection problem.

Proposition.

There exists a shortest path from s to v in an edge-weighted digraph if and only if there exists at least one directed path from s to v and no vertex on any directed path from s to v is on a negative cycle.

Proposition.

The Bellman-Ford algorithm solves the single-source shortest-paths problem from a given source s (or finds a negative cycle reachable from s) for any edge-weighted digraph with V vertices and E edges, in time proportional to E V and extra space proportional to V, in the worst case.

Q + A

Q. Does Dijkstra's algorithm work with negative weights?

A. Yes and no. There are two shortest paths algorithms known as Dijkstra's algorithm, depending on whether a vertex can be enqueued on the priority queue more than once. When the weights are nonnegative, the two versions coincide (as no vertex will be enqueued more than once). The version implemented in DijkstraSP.java (which allows a vertex to be enqueued more than once) is correct in the presence of negative edge weights (but no negative cycles) but its running time is exponential in the worst case. (We note that DijkstraSP.java throws an exception if the edge-weighted digraph has an edge with a negative weight, so that a programmer is not surprised by this exponential behavior.) If we modify DijkstraSP.java so that a vertex cannot be enqueued more than once (e.g., using a marked[] array to mark those vertices that have been relaxed), then the algorithm is guaranteed to run in E log V time but it may yield incorrect results when there are edges with negative weights.

Exercises

True or false. Adding a constant to every edge weight does not change the solution to the single-source shortest-paths problem.
Solution. False.
Provide an implementation of toString() for EdgeWeightedDigraph.java.
Use the memory-cost model of Section 1.4 to determine the amount of memory used by EdgeWeightedDigraph.java to represent a graph with V vertices and E edges.
Solution. 56 + 40V + 72E. MemoryOfEdgeWeightedDigraph.java computes it empirically assuming that no Integer values are cached—Java typically caches the integers -128 to 127.
Adapt the DirectedCycle and Topological classes from Section 4.2 to use the EdgeweightedDigraph and DirectedEdge APIs of this section, thus implementing EdgeWeightedDirectedCycle.java and Topological.java.
Suppose that we convert an EdgeWeightedGraph into an EdgeWeightedDigraph by creating two DirectedEdge objects in the EdgeWeightedDigraph (one in each direction) for each Edge in the EdgeWeightedGraph and then use the Bellman-Ford algorithm. Explain why this approach fails spectacularly.
Solution: This can introduce negative cost cycles even if the edge-weighted graph does not contain them.
What happens if you allow a vertex to be enqueued more than once in the same pass in the Bellman-Ford algorithm?
Answer: The running time of the algorithm can go exponential. For example, consider what happens for the complete edge-weighted digraph whose edge weights are all -1.

Creative Problems

Longest paths in DAGs. Develop an implementation AcyclicLP.java that can solve the longest-paths problem in edge-weighted DAGs.
All-pairs shortest paths on a line. Given a weighted line-graph (undirected connected graph, all vertices of degree 2, except two endpoints which have degree 1), devise an algorithm that preprocesses the graph in linear time and can return the distance of the shortest path between any two vertices in constant time.
Partial solution. Find a vertex s of degree 1 and run breadth-first (or depth-first) search to find the order in which the remaining vertices appear. Then, compute the length of the shortest path from s to v for each vertex v, say dist[v]. The shortest path between v and w is |dist[v] - dist[w]|.
Monotonic shortest path. Given an edge-weighted digraph, find a monotonic shortest path from s to every other vertex. A path is monotonic if the weight of every edge on the path is either strictly increasing or strictly decreasing.
Partial solution: relax edges in ascending order and find a best path; then relax edges in descending order and find a best path.
Lazy implementation of Dijkstra's algorithm. Develop an implementation LazyDijkstraSP.java of the lazy version of Dijkstra's algorithm that is described in the text.
Bellman-Ford queue never empties. Show that if there is a negative cycle reachable from the source in the queue-based implementation of the Bellman-Ford algorithm, then the queue never empties.
Solution: Consider a negative cycle and suppose that distTo[w] <= distTo[v] + length(v, w) for all edges on cycle W. Summing up this inequality for all edges on the cycle implies that the length of the cycle is nonnegative.
Bellman-Ford negative cycle detection. Show that if any edge is relaxed during the Vth pass of the generic Bellman-Ford algorithm, then the edgeTo[] array has a directed cycle and any such cycle is a negative cycle.
Solution: todo.

Web Exercises

Optimal substructure property. Prove that every subpath on a shortest path from v to w is also a shortest path between the two endpoints.
Unique shortest path tree. Suppose that there is a unique shortest path from s to every other vertex. Prove that the SPT is unique.
No negative cycles. Prove that if the generic algorithm terminates, then there are no negative cycles reachable from s. Hint: upon termination, all edges reachable from s satisfy distTo[w] <= distTo[v] + e.weight(). Add up this inequality for all edges along a cycle.
Predecessor graph. True or false. During execution of Bellman-Ford in an edge-weighted digraph with no negative cycles, following the edgeTo[] array always yields a path back to s. Repeat the question for Dijkstra's algorithm.
Yen's improvement to Bellman-Ford. [reference] Partition the edges into two DAGs A and B: A consists of edges that go from a lower indexed vertex to a higher indexed vertex; B consists of edges that go from a higher indexed vertex to a lower indexed vertex. When iterating through all of the edges in a phase of Bellman-Ford, first iterate through the edges in A in ascending order of vertex number (a topological order of A), then iterate through the edges in B in descending order of vertex number (a topological order of B). When iterating through the edges in A, any path in the SPT that starts at a vertex with the correct distTo[] value and uses only edges in A results in the correct distTo[] value; similarly for B. The number of passes needed is the maximum number of A-B alternations on a path, which is at most (V+1)/2. Thus, the number of passes is at most (V+1)/2 instead of V.
Replacement paths. Given an edge-weighted digraph with nonnegative weights and source s and sink t, design an algorithm to find the shortest path from s to t that does not use edge e for every edge e. The order of growth of your algorithm should be E V log V.
Road network data sets.
- From the DIMACS challenge. Here are all the roads in each state.
- rome99.txt is a large portion of the directed road network of Rome from the DIMACS challenge. The graph contains 3353 vertices and 8870 edges. Vertices correspond to intersections between roads and edges correspond to roads or road segments. The edge weights are distances in meters.
- NYC.txt is the undirected road network of New York City. The graph contains 264346 vertices and 733846 edges. It is connected, contains parallel edges, but no self-loops. The edge weights are travel times and are strictly positive.
Internet routing. OSPF (Open Shortest Path First) is a widely used protocol for Internet routing that uses Dijkstra's algorithm. RIP (Routing Information Protocol) is another routing protocol based on the Bellman-Ford algorithm.
Shortest path with the ability to skip one edge. Given an edge-weighted digraph with nonnegative weights, Design an E log V algorithm for finding the shortest path from s to t where you have the option to change the weight of any one edge to 0.
Solution. Compute the shortest path from s to every other vertex; compute the shortest path from every vertex to t. For each edge e = (v, w), compute the sum of the length of the shortest path from s to v and the length of the shortest path from w to t. The smallest such sum provides the shortest such path.
Shortest paths in undirected graphs. Write a program DijkstraUndirectedSP.java that solves the single-source shortest paths problems in undirected graphs with nonnegative weights using Dijkstra's algorithm.
Floyd-Warshall algorithm. FloydWarshall.java implements the Floyd-Warshall algorithm for the all-pairs shortest path problem. It takes time proportional to V^3 and space proportional to V^2. It uses AdjMatrixEdgeWeightedDigraph.java.
Randomized Bellman-Ford. [reference] Suppose that we choose the vertex order in Yen's algorithm uniformly at randomly (where A contains all the edges that go from a lower vertex in the permutation to a higher vertex). Prove that the expected number of passes is at most (V+1)/3.
Suurballe's algorithm. Given a digraph with non-negative edge weights and two distinguished vertices s and t, find two edge-disjoint paths from s to t such that the sum of the weights of the two paths is minimized.
Solution. This can be done with a clever application of Dijkstra's algorithm, known as Suurballe's algorithm.