2.5 Sorting Applications
Sorting algorithms and priority queues are widely used in a
broad variety of applications. Our purpose in this section
is to briefly survey some of these applications.
Sorting various types of data.
Our implementations sort arrays of Comparable objects. This Java convention allows us to use Java's callback mechanism to sort arrays of objects of any type that implements the Comparable interface.- Transaction example. Program Transaction.java implements the Comparable interface for a transaction data type based on when the transaction occurred.
- Pointer sorting. The approach we are using is known in the classical literature as pointer sorting, so called because we process references to keys and do not move the data itself.
- Keys are immutable. It stands to reason that an array might not remain sorted if a client is allowed to change the values of keys after the sort. In Java, it is wise to ensure that key values do not change by using immutable keys.
- Exchanges are inexpensive. Another advantage of using references is that we avoid the cost of moving full items. The reference approach makes the cost of an exchange roughly equal to the cost of a compare for general situations.
- Alternate orderings. There are many applications where we want to use two different orders for the objects that we are sorting, depending upon the situation. The Java Comparator interface has a single public method compare() that compares two objects. If we have a data type that implements this interface, we can pass a Comparator to sort() (which passes it to less()) as in Insertion.java.
- Items with multiple keys. In typical applications, items have multiple instance variables that might need to serve as sort keys. In our transaction example, one client may need to sort the transaction list by account number; another client might need to sort the list by place; and other clients might need to use other fields as sort keys. We can define multiple comparators, as in Transaction.java.
- Priority queues with comparators. The same flexibility to use comparators is also useful for priority queues. MaxPQ.java and MinPQ.java include a constructor that takes a Comparator as an argument.
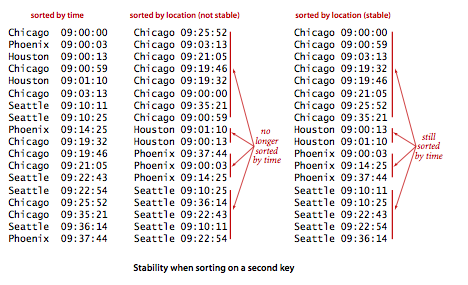
- Stability.
A sorting method is stable if it preserves the relative
order of equal keys in the array.
For example, suppose, in our internet
commerce application, that we enter transactions into an array as they
arrive, so they are in order of the time field in the array. Now suppose that the
application requires that the transactions be separated out by location for further
processing. One easy way to do so is to sort the array by location. If the sort is unstable,
the transactions for each city may not necessarily be in order by time
after the sort. Some of the sorting methods that we have considered in
this chapter are stable (insertion sort and mergesort); many
are not (selection sort, shellsort, quicksort, and heapsort).
Which sorting algorithm should I use?
Knowing which algorithm is best possible depends heavily on details of the application and implementation, but we have studied some general-purpose methods that can be nearly as effective as the best possible for a wide variety of applications. The following table is a general guide that summarizes the important characteristics of the sort algorithms that we have studied in this chapter.
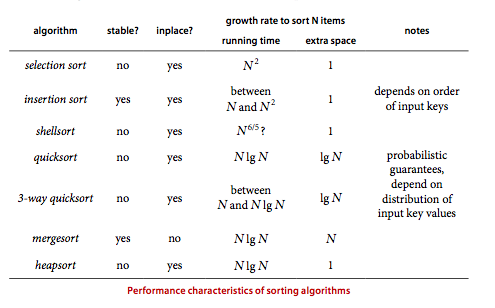
Property. Quicksort is the fastest general-purpose sort.
In most practical situations, quicksort is the method of choice. If stability is important and space is available, mergesort might be best. In some performance-critical applications, the focus may be on just sorting numbers, so it is reasonable to avoid the costs of using references and sort primitive types instead.
- Sorting primitive types. We can develop more efficient versions of our sort codes for sorting primitive types by replacing Comparable with the primitive type name, and replacing calls to less() with code like a[i] < a[j]. However, some care is needed with floating-point types to deal with -0.0 and NaN.
- Java system sort.
Java's primary system sort method Arrays.sort() in the java.util library
represents a collection of overloaded methods:
- A different method for each primitive type.
- A method for data types that implement Comparable.
- A method that uses a Comparator.
Java's systems programmers have chosen to use quicksort (with 3-way partitioning) to implement the primitive-type methods, and mergesort for reference-type methods. The primary practical implications of these choices are to trade speed and memory usage (for primitive types) for stability and guaranteed performance (for reference types).
Reductions.
The idea that we can use sorting algorithms to solve other problems is an example of a basic technique in algorithm design known as reduction. A reduction is a situation where an algorithm developed for one problem is used to solve another. We begin with a few elementary examples for sorting.- Duplicates. Are there any duplicate keys in an array of Comparable objects? How many distinct keys are there in an array? Which value appears most frequently? With sorting, you can answer these questions in linearithmic time: first sort the array, then make a pass through the sorted array, taking note of duplicate values that appear consecutively in the ordered array.
- Rankings. A permutation (or ranking) is an array of N integers where each of the integers between 0 and N-1 appears exactly once. The Kendall tau distance between two rankings is the number of pairs that are in different order in the two rankings. For example the Kendall tau distance between 0 3 1 6 2 5 4 and 1 0 3 6 4 2 5 is four because the pairs 0-1, 3-1, 2-4, 5-4 are in different order in the two rankings, but all other pairs are in the same order.
- Priority queue reductions. In Section 2.4, we considered two examples of problems that reduce to a sequence of operations on priority queues. TopM.java finds the M items in an input stream with the highest keys. Multiway.java merges together M sorted input streams to make a sorted output stream. Both of these problems are easily addressed with a priority queue of size M.
- Median and order statistics.
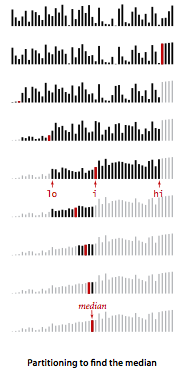 An important application related to sorting
is the operation of finding the median of a set of
keys (the value with the property that half the keys are no
larger and half the keys are no smaller). This
operation is a common computation in statistics and in various other
data-processing applications.
Finding the median is a special case of selection:
finding the kth smallest of a set of numbers.
It is easy to solve the problem in linearithmic time by sorting.
The method select()
An important application related to sorting
is the operation of finding the median of a set of
keys (the value with the property that half the keys are no
larger and half the keys are no smaller). This
operation is a common computation in statistics and in various other
data-processing applications.
Finding the median is a special case of selection:
finding the kth smallest of a set of numbers.
It is easy to solve the problem in linearithmic time by sorting.
The method select()
We describe an approach that solves the problem in linear time: Maintain the variables lo and hi to delimit the subarray that contains the index k of the item to be selected and use use quicksort partitioning to shrink the size of the subarray, as follows:
- If k is equal to j, then we are done.
- Otherwise, if k < j, then we need to continue working in the left subarray (by changing the value of hi to j-1)
- Otherwise, if k > j, then we need to continue working in the right subarray (by changing lo to j+1).
The interval shrinks until it consists just of k. Upon termination a[k] contains the (k+1)st smallest entry, a[0] through a[k-1] are all small than (ore equal to) a[k], and a[k+1] through the end of the array are all larger than (or equal to) a[k].
The select() method in Quick.java implements this approach, but it requires a cast in the client. The select() method in QuickPedantic.java is more pedantic code that obviates the need for a cast.
A brief survey of sorting applications.
- Commercial computing. Government organizations, financial institutions, and commercial enterprises organize much of this information by sorting it. Whether the information is accounts to be sorted by name or number, transactions to be sorted by time or place, mail to be sorted by postal code or address, files to be sorted by name or date, or whatever, processing such data is sure to involve a sorting algorithm somewhere along the way.
- Search for information. Keeping data in sorted order makes it possible to efficiently search through it using the classic binary search algorithm.
- Operations research. Suppose that we have N jobs to complete, where job j requires tj seconds of processing time. We need to complete all of the jobs, but want to maximize customer satisfaction by minimizing the average completion time of the jobs. The shortest processing time first rule, where we schedule jobs in increasing order of processing time, is known to accomplish this goal. As another example, consider the load-balancing problem, where we have M identical processors and N jobs to complete, and our goal is to schedule all of the jobs on the processors so that the time when the last job completes is as early as possible. This specific problem is NP-hard (see Chapter 6) so we do not expect to find a practical way to compute an optimal schedule. One method that is known to produce a good schedule is the longest processing time first rule, where we consider the jobs in decreasing order of processing time, assigning each job to the processor that becomes available first.
- Event-driven simulation. Many scientific applications involve simulation, where the point of the computation is to model some aspect of the real world in order to be able to better understand it. Doing such simulations efficiently can require appropriate algorithms and data structures. We consider a particle-collision simulation in Section 6.1 that illustrates this point.
- Numerical computations. Scientific computing is often concerned with accuracy (how close are we to the true answer?). Accuracy is extremely important when we are performing millions of computations with estimated values such as the floating-point representation of real numbers that we commonly use on computers. Some numerical algorithms use priority queues and sorting to control accuracy in calculations.
- Combinatorial search. A classic paradigm in artificial intelligence is to define a set of configurations with well-defined moves from one configuration to the next and a priority associated with each move. Also defined is a start configuration and a goal configuration (which corresponds to having solved the problem. The A* algorithm is a problem-solving process where we put the start configuration on the priority queue, then do the following until reaching the goal: remove the highest-priority configuration and add to the queue all configurations that can be reached from that with one move (excluding the one just removed).
- Prim's algorithm and Dijkstra's algorithm are classical algorithms that process graphs. Priority queues play a fundamental role in organizing graph searches, enabling efficient algorithms.
- Kruskal's algorithm is another classic algorithm for graphs whose edges have weights that depends upon processing the edges in order of their weight. Its running time is dominated by the cost of the sort.
- Huffman compression is a classic data compression algorithm that depends upon processing a set of items with integer weights by combining the two smallest to produce a new one whose weight is the sum of its two constituents. Implementing this operation is immediate, using a priority queue.
- String processing algorithms are often based on sorting. For example, we will discuss algorithms for finding the longest common prefix among a set of strings and the longest repeated substring in a given string that are based on first sorting suffixes the strings.
Exercises
-
Consider the following implementation of the compareTo()
method for String. How does the third line help with efficiency?
public int compareTo(String t) { String s = this; if (s == t) return 0; // this line int n = Math.min(s.length(), t.length()); for (int i = 0; i < n; i++) { if (s.charAt(i) < t.charAt(i)) return -1; else if (s.charAt(i) > t.charAt(i)) return +1; } return s.length() - t.length(); }Solution: it avoid directly comparing individual characters if s and t are references to the same string.
-
Criticize the following implementation of a class intended to
represent customer account balances.
Why is compareTo() a flawed implementation of the
Comparable interface?
public class Customer implements Comparable<Customer> { private String name; private double balance; public int compareTo(Customer that) { if (this.balance < that.balance - 0.005) return -1; if (this.balance > that.balance + 0.005) return +1; return 0; } }Solution: it violates the Comparable contract. It is possible that a.compareTo(b) and b.compareTo(c) are both 0, but a.compareTo(c) is positive (or negative).
-
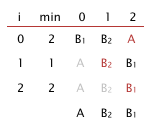
Explain why selection sort is not stable.
Solution. It exchanges nonadjacent elements. On the example below, the first B gets swapped to the right of the second B.
- Write a program Frequency.java that reads strings from standard input and prints the number of times each string occurs, in descending order of frequency.
Creative Problems
- Scheduling. Write a program SPT.java that reads job names and processing times from standard input and prints a schedule that minimizes average completion time, as described in the text.
- Load balancing.
Write a program LPT.java
that takes an integer M as a command-line argument, reads N job names
and processing times from standard input and prints a scheduling
assignment the jobs to M processors that approximately minimizes
the time when the last job completes, as described in the text.
Remark. The resulting solution is guaranteed to be within 33% of the best possible (actually 4/3 - 1/(3N)).
- Sort by reverse domain. Write a data type Domain.java that represents domain names, including an appropriate compareTo() method where the natural order is in order of the reverse domain name. For example, the reverse domain of cs.princeton.edu is edu.princeton.cs. This is useful for web log analysis. Write a client that reads domain names from standard input and prints the reverse domains in sorted order.
- Spam campaign. To initiate an illegal spam campaign, you have a list of email addresses from various domains (the part of the email address that follows the @ symbol). To better forge the return addresses, you want to send the email from another user at the same domain. For example, you might want to forge an email from wayne@princeton.edu to rs@princeton.edu. How would you process the email list to make this an efficient task?
- Unbiased election.
In order to thwart bias against candidates whose names appear toward the end
of the alphabet, California sorted the candidates appearing on its 2003
gubernatorial ballot by using the following order:
R W Q O J M V A H B S G Z X N T C I E K U P D Y F L
Create a data type California.java where this is the natural order. Write a client that sorts strings according to this ordering. Assume that each string is comprised solely of uppercase letters.
- Kendall tau distance. Write a program KendallTau.java that computes the Kendall tau distance between two permutations in linearithmic time.
- Stable priority queue. Develop a stable priority-queue implementation StableMinPQ.java (which returns duplicate keys in the same order in which they were inserted).
- Points in the plane. Write three static static comparators for the Point2D.java data type, one that compares points by their x coordinate, one that compares them by their y coordinate, and one that compares them by their distance from the origin. Write two non-static comparators for the Point2D data type, one that compares them by their distance to a specified point and one that compares them by their polar angle with respect to a specified point.
- Interval 1D data type. Write three static comparators for Interval1D.java, one that compares intervals by their left endpoing, one that compares intervals by their right endpoint, and one that compares intervals by their length.
- Sort files by name. Write a program FileSorter.java that takes the name of a directory as a command line input and prints out all of the files in the current directory, sorted by filename. Hint: use the java.io.File data type.
- Boerner's theorem. True or false: If you sort each column of a matrix, then sort each row, the columns are still sorted. Justify your answer.
- Distinct values. Write a program Distinct.java that takes integers M, N, and T as command-line arguments, then uses the code given in the text to perform T trials of the following experiment: Generate N random int values between 0 and M–1 and count the number of distinct values generated. Run your program for T = 10 and N = 10^3, 10^4, 10^5, and 10^6, with M = 1/2 N, N, and 2N. Probability theory says that the number of distinct values should be about M(1 – e^(-alpha)), where alpha = N/M— print a table to help your confirm that your experiments validate this formula.
Web Exercises
- Counter data type. Modify Counter.java so that it implements the Comparable interface, comparing counters by tally.
- Grade data type. Write a program Grade.java to represent a data type for grades (A, B+, etc.). It should implement the Comparable interface using the natural ordering on grades by GPA.
- Student data type. Write an data type Student.java that represents a student in a college course. Each student should have a login (String), a section number (integer), and a grade (Grade).
- Case insensitive order.
Write a code fragment to read in a sequence of strings and
sort them in ascending order, ignoring case.
String[] a = new String[N]; for (int i = 0; i < N. i++) { a[i] = StdIn.readString(); } Arrays.sort(a, String.CASE_INSENSITIVE_ORDER); - Case insensitive comparator.
Implement your own version of the
comparator String.CASE_INSENSITIVE_ORDER.
public class CaseInsensitive implements Comparator<String> { public int compare(String a, String b) { return a.compareToIgnoreCase(b); } } - Descending order string comparator.
Implement a comparator that sorts string
in descending order instead of ascending order.
Alternatively, you can use Collections.reverseOrder(). It returns a Comparator that imposes the reverse of the natural ordering of objects that implement the Comparable interface.public class Descending implements Comparator<String> { public int compare(String a, String b) { return b.compareToIgnoreCase(a); } } - Sorting strings from non-English alphabets.
Write a program to sort strings according to non-English alphabets,
for accents, umlauts, and pre-composed character
like ch in Spanish.
Hint: Use Java's java.text.Collator API. For example in UNICODE, Rico occurs lexicographically before Réal, but in French, Réal occurs first.
import java.util.Arrays; import java.text.Collator; ... Arrays.sort(words, Collator.getInstance(Locale.FRENCH));
- Smith's rule. The following problem arises in supply chain management. You have a bunch of jobs to schedule on a single machine. (Give example.) Job j requires p[j] units of processing time. Job j has a positive weight w[j] which represents its relative importance - think of it as the inventory cost of storing the raw materials for job j for 1 unit of time. If job j finishes being processed at time t, then it costs t * w[j] dollars. The goal is to sequence the jobs so as to minimize the sum of the weighted completion times of each job. Write a program SmithsRule.java that reads in a command line parameter N and a list of N jobs specified by their processing time p[j] and their weight w[j], and output an optimal sequence in which to process their jobs. Hint: Use Smith's rule: schedule the jobs in order of their ratio of processing time to weight. This greedy rule turns out to be optimal.
- Rhyming words.
For your poetry class, you would like to tabulate a list of
rhyming words. A crude way to accomplish this task is as follows:
- Read in a dictionary of words into an array of strings.
- Reverse the letters in each word, e.g., confound becomes dnuofnoc.
- Sort the resulting array of words.
- Reverse the letters in each word back to their original state.
Now the word confound will be next to words like astound and compound. Write a program Rhymer.java that reads in a sequence of words from standard input and prints them out in the order specified above.
Now repeat, but use a customized Comparator that sorts lexicographically from right-to-left.
- Mode. Give an O(N log N) algorithm for computing the mode (value that occurs most frequently) of a sequence of N integers.
- Closest 1d pair. Given a sequence of N real numbers, find the pair of integers that are closest in value. Give a O(N log N) algorithm.
- Farthest 1d pair. Given a sequence of N real numbers, find the pair of integers that are farthest apart in value. Give a O(N) algorithm.
- Sorting with many duplicates. Suppose you have a sequence of N elements, with at most log N distinct ones. Describe how to sort them in O(N log log N) time.
- Nearly sorted. Given an array of N elements, each which is at most k positions from its target position, devise an algorithm that sorts in O(N log k) time.
- Sorting a linked list. Given a singly linked list of N elements, how could you sort it in guaranteed O(N log N) time, stably, and with O(1) extra space?
- Goofysort (Jim Huggins). Argue that Goofy.java sorts the array in ascending order. What is the best-case running time of as a function of the number of items to be sorted N? What is the worst-case running time of as a function of the number of items to be sorted N?
- Feel-good interval.
Given an array of N nonnegative integers (representing a person's
emotional value on each day), the
happiness in an interval is the sum of the values in that interval
multiplied by the smallest integer in that interval.
Design an O(N log N) divide-and-conquer
algorithm to find the happiest interval.
Solution. Here's a mergesort style solution.
- Divide the elements in the middle: a[l..m-1], a[m], a[m+1..r]
- Recursively compute the optimal interval entirely in the left half
- Recursively compute the optimal interval entirely in the right half
- Compute the optimal interval containing a[m]
- Return the best of the three intervals
- Equality detector. Suppose that you have N elements and you want to determine if at least N/2 are equal. Assume the only operation on the elements you can perform is equality testing. Design an algorithm that performs O(N log N) equality tests to find a representative element if it exists. Hint: divide-and-conquer. Note: can also do in O(N) tests.
- Maxima. Given a set of n points in the plane, point (xi, yi) dominates (xj, yj) if xi > xj and yi > yj. A maxima is a point that is not dominated by any other point in the set. Devise an O(n log n) algorithm to find all maxima. Application: on x-axis is space efficiency, on y-axis is time efficiency. Maxima are useful algorithms. Hint: sort in ascending order according to x-coordinate; scan from right to left, recording the highest y-value seen so far, and mark these as maxima.
- Min and max.
Given an array of N elements, find the min and max using
as few compares as possible.
Brute force: find the max (N-1 compares), then
find the min of the remaining elements (N-2 compares).
Solution 1. Divide and conquer: find min and max in each half (2T(N/2) compares), return min of 2 and max of 2 (2 compares). T(1) = 0, T(2) = 1, T(N) = 2T(N/2) + 2. Recurrence solution: T(N) = ceil(3N/2) - 2.
Solution 2. Divide the elements into pairs and compare two elements in each pair. Put the smallest elements in A and the largest in B. If n is odd, put element n in both A and B. This requires floor(n/2) comparisons. Now directly compute the minimum in A (ceil(n/2) - 1 comparisons) and the maximum in B (ceil(N/2) - 1) comparisons. [In fact, this is best possible.]
- Sorting by reversals. [ Mihai Patrascu] Given an array a[1..n], sort using the following type operation: pick two indices i and j and reverse the elements in a[i..j]. This operation costs j-i+1. Goal: O(n log^2 n).
- L1 norm. There are N circuit elements in the plane. You need to run a special wire (parallel to the x-axis) across the circuit. Each circuit element must be connected to the special wire. Where should you put the special wire? Hint: median minimizes L1 norm.
- Median given two sorted arrays. Given two sorted arrays of size N1 and N2, find the median of all elements in O(log N) time where N = N1 + N2. Or find the kth overall largest in O(log k).
- Three nearby numbers in an array.
Given a floating-point array a[], design a linearithmic algorithm
to find three distinct integers i, j, and k such that
|a[i] - a[j]| + |a[j] - a[k]| + |a[k] - a[i]| is minimum.
Hint: if a[i] <= a[j] <= a[k], then |a[i] - a[j]| + |a[j] - a[k]| + |a[k] - a[i]| = 2 (a[k] - a[i]).
- Three nearby numbers in three arrays. Given three floating-point arrays a[], b[], and c[], design a linearithmic algorithm to find three integers i, j, and k such that |a[i] - b[j]| + |b[j] - c[k]| + |c[k] - a[i]| is minimum.
- Minimum dot product. Given two vectors of the same length, find a permutation of the two vectors such that the dot product of the two vectors is as small as possible.
- Two-sum.
Given an array of N integers, design a linearithmic algorithm to
find a pair of integers whose sum is closest to zero.
Solution: sort by absolute value—the best pair is now adjacent.
- 3-sum in quadratic time.
The 3-sum problem is to find, in an array of integers,
the triple whose sum is closest to zero.
Describe an algorithm for this problem that uses linear space
and quadratic time.
Hint: solve the following subproblem. Given a sorted list of N integers and a target integer x, determine in linear time the two whose sum is closest to x.
- Bandwidth.
Given intervals with bandwidth requirements, find the maximum bandwidth
requirement (and the interval for which that maximum is required).
Solution. Sort the intervals by start time; insert the intervals into PQ in this order, but using the ending time as the key. Before inserting the next interval, compare its start time to ending time of the minimum interval on the PQ: if it is greater, delete the minimum interval on the PQ. Always keep track of the cumulative bandwidth on the PQ.
- Time stamps. Given N time stamps when file is requested from web server, find largest interval of time at which no file arrives. Solution: sort by time stamp. Scan sorted list to identify maximum gap. (Same as idle time.)
- Ticket ranges. Given a list of ticket seats of the form A1, A2, A11, A10, B7, B9, B8, B3, find the largest non-empty block of adjacent seats, e.g., A3-A9. (Same as idle time.)
- Decimal dominant.
Given an array with N comparable keys,
design an algorithm to check if there is a value that appears more than N/10 times.
Your algorithm should run in expected linear time.
Solution. Use quickselect to find the N/10th largest value; check if it is a dominant; if not, recur in the subarray with 9N/10 values.
Alternatively, use 9 counters.
- Local min and max.
Given N distinct comparable items, rearrange them so that each internal
item is either greater than both
items right before and after it or less than both items right before and after it.
Hint: sort and interleave the first and second halves.
- h-index.
Given an array of N positive integers,
its h-index
is the largest integer h such that there are at least h
entries in the array greater than or equal to h.
Design an algorithm to compute the h-index of an array.
Hint: median or quicksort-like partitioning and divide-and-conquer.
- Software version number. Define a comparator that compares two version numbers (such as 1.2.32 and 1.2.5) chronologically. Assume that the version number is a string composed of only decimal digits and . character. The . character separates fields; it is not a decimal point.
- Stable selection sort.
What modifications do you need to do to make selection sort stable?
Solution: first, when finding the minimum remaining key, always choose the leftmost entry; second, instead of moving the minimum key to the front with one exchange, move all elements to its left that are large one position to the right.
- Largest number.
Given n positive integers, concatenate them so that they form the largest number.
For example, if the numbers are 123, 12, 96, and 921, then
the result should be 9692112312.
Solution. Define a comparator that compares two numbers by concatenating them together in either order (e.g., for 96 and 921, compare 96921 vs. 92196) and seeing which string is lexicographically largest.
- Largest number. Given three arrays A, B, and C, each of length n, determine ther number of triples with a in A, b in B, and c in C are there such that a < b < c?


