6.1 Event-Driven Simulation
This chapter under construction.
Simulate the motion of N colliding particles according to the laws of elastic collision using event-driven simulation. Such simulations are widely used in molecular dynamics (MD) to understand and predict properties of physical systems at the particle level. This includes the motion of molecules in a gas, the dynamics of chemical reactions, atomic diffusion, sphere packing, the stability of the rings around Saturn, the phase transitions of cerium and cesium, one-dimensional self-gravitating systems, and front propagation. The same techniques apply to other domains that involve physical modeling of particle systems including computer graphics, computer games, and robotics. We will revisit some of these issues again in Chapter 7.
Hard sphere model. The hard sphere model (billiard ball model) is an idealized model of the motion of atoms or molecules in a container. We focus on the two-dimensional version called the hard disc model. The salient properties of this model are listed below.
- N particles in motion, confined in the unit box.
- Particle i has known position (rxi, ryi), velocity (vxi, vyi), mass mi, and radius σi.
- Particles interact via elastic collisions with each other and with the reflecting boundary.
- No other forces are exerted. Thus, particles travel in straight lines at constant speed between collisions.
Simulation. There are two natural approaches to simulating the system of particles.
- Time-driven simulation. Discretize time into quanta of size dt. Update the position of each particle after every dt units of time and check for overlaps. If there is an overlap, roll back the clock to the time of the collision, update the velocities of the colliding particles, and continue the simulation. This approach is simple, but it suffers from two significant drawbacks. First, we must perform N2 overlap checks per time quantum. Second, we may miss collisions if dt is too large and colliding particles fail to overlap when we are looking. To ensure a reasonably accurate simulation, we must choose dt to be very small, and this slows down the simulation.
- Event-driven simulation.
With event-driven simulation we focus only on those times at which
interesting events occur.
In the hard disc model, all particles travel in straight line
trajectories at constant speeds between collisions.
Thus, our main challenge is to determine the ordered sequence of
particle collisions.
We address this challenge by maintaining a priority queue of
future events, ordered by time.
At any given time, the priority queue contains all future
collisions that would occur, assuming each particle
moves in a straight line trajectory forever.
As particles collide and change direction, some of the events
scheduled on the priority queue become "stale" or "invalidated",
and no longer correspond to physical collisions.
We adopt a lazy strategy, leaving such invalidated collision on the priority
queue, waiting to identify and discard them as they are deleted.
The main event-driven simulation loop works as follows:
- Delete the impending event, i.e., the one with the minimum priority t.
- If the event corresponds to an invalidated collision, discard it. The event is invalid if one of the particles has participated in a collision since the time the event was inserted onto the priority queue.
- If the event corresponds to a physical collision between particles
i and j:
- Advance all particles to time t along a straight line trajectory.
- Update the velocities of the two colliding particles i and j according to the laws of elastic collision.
- Determine all future collisions that would occur involving either i or j, assuming all particles move in straight line trajectories from time t onwards. Insert these events onto the priority queue.
- If the event corresponds to a physical collision between particles i and a wall, do the analogous thing for particle i.
This event-driven approach results in a more robust, accurate, and efficient simulation than the time-driven one.
Collision prediction. We review the formulas that specify if and when a particle will collide with the boundary or with another particle, assuming all particles travel in straight-line trajectories.
- Collision between particle and a wall.
Given the position (rx, ry), velocity
(vx, vy), and radius σ of
a particle at time t, we wish to determine if and when it
will collide with a vertical or horizontal wall.
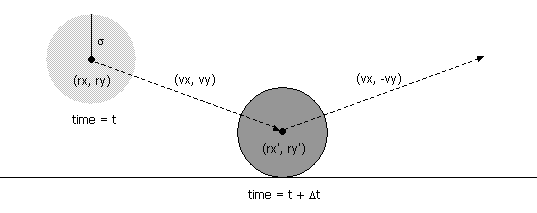
Since the coordinates are between 0 and 1, a particle comes into contact with a horizontal wall at time t + Δt if the quantity ry + Δt vy equals either σ or (1 - σ). Solving for Δt yields:
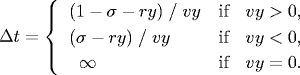
An analogous equation predicts the time of collision with a vertical wall.
- Collision between two particles.
Given the positions and velocities of two particles i and j
at time t,
we wish to determine if and when they will collide with each other.
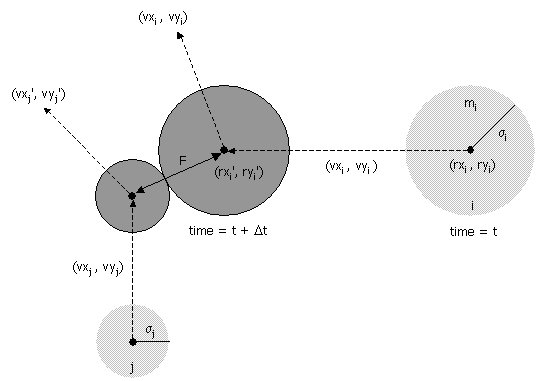
Let (rxi' , ryi' ) and (rxj' , ryj' ) denote the positions of particles i and j at the moment of contact, say t + Δt. When the particles collide, their centers are separated by a distance of σ = σi + σj. In other words:
σ2 = (rxi' - rxj' )2 + (ryi' - ryj' )2
During the time prior to the collision, the particles move in straight-line trajectories. Thus,rxi' = rxi + Δt vxi, ry i' = ryi + Δt vyi
Substituting these four equations into the previous one, solving the resulting quadratic equation for Δt, selecting the physically relevant root, and simplifying, we obtain an expression for Δt in terms of the known positions, velocities, and radii.
rxj' = rxj + Δt vxj, ry j' = ryj + Δt vyj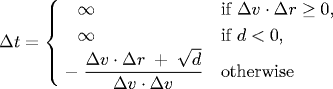
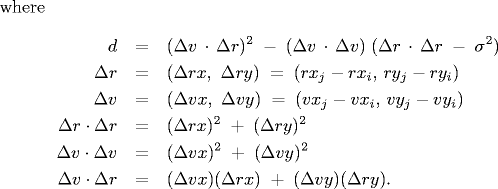
If either Δv ⋅ Δr ≥ 0 or d < 0, then the quadratic equation has no solution for Δt > 0; otherwise we are guaranteed that Δt ≥ 0.
Collision resolution. In this section we present the physical formulas that specify the behavior of a particle after an elastic collision with a reflecting boundary or with another particle. For simplicity, we ignore multi-particle collisions. There are three equations governing the elastic collision between a pair of hard discs: (i) conservation of linear momentum, (ii) conservation of kinetic energy, and (iii) upon collision, the normal force acts perpendicular to the surface at the collision point. Physics-ly inclined students are encouraged to derive the equations from first principles; the rest of you may keep reading.
- Between particle and wall. If a particle with velocity (vx, vy) collides with a wall perpendicular to x-axis, then the new velocity is (-vx, vy); if it collides with a wall perpendicular to the y-axis, then the new velocity is (vx, -vy).
- Between two particles.
When two hard discs collide, the normal force acts along
the line connecting their centers (assuming no friction or spin).
The impulse (Jx, Jy) due to the normal force in the
x and y directions of a perfectly elastic collision
at the moment of contact is:
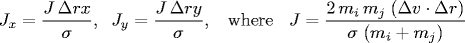
and where mi and mj are the masses of particles i and j, and σ, Δx, Δy and Δ v ⋅ Δr are defined as above. Once we know the impulse, we can apply Newton's second law (in momentum form) to compute the velocities immediately after the collision.
vxi' = vxi + Jx / mi, vxj' = vxj - Jx / mj
vyi' = vyi + Jy / mi, vyj' = vyj - Jy / mj
Particle collision simulation in Java. Our implementation involves the following data types: MinPQ.java, Particle.java, and CollisionSystem.java.
- Particle data type. Represents particles moving in the unit box.
- Event data type.
Data type that represents collision events. There are
four different types of events: a collision with a vertical wall,
a collision with a horizontal wall, a collision between two particles,
and a redraw event. This would be a fine opportunity to experiment
with OOP and polymorphism. We propose the following simpler
(but somewhat less elegant approach).
In order to implement isValid, the event data type should store the collision counts of the relevant particles at the time the event was created. The event corresponds to a physical collision if the current collision counts of the particles are still the same as when the event was created, i.e., no intervening collisions.
Data files. We use the following data format. The first line contains the number of particles N. Each of the remaining N lines consists of 6 real numbers (position, velocity, mass, and radius) followed by three integers (red, green, and blue values of color). You may assume that all of the position coordinates are between 0 and 1, and the color values are between 0 and 255. Also, you may assume that none of the particles intersect each other or the walls.
Here are some sample data files:
FILE
DESCRIPTION
p10.txt
10 particles
p2000.txt
2000 particles
diagonal.txt
diagonal1.txt
diagonal2.txt
wallbouncing.txt
9 particles in a row colliding with 9 particles in a column
wallbouncing2.txt
10 particles in a row not colliding with 9 particles in a column
wallbouncing3.txt
19 particles in a row colliding with 19 particles in a column
p100-.125K.txt
100 particles at 0.125 Kelvin
p100-.5K.txt
100 particles at 0.5 Kelvin
p100-2K.txt
100 particles at 2.0 Kelvin
p1000-.5K.txt
1000 particles at 0.5 Kelvin
p1000-2K.txt
1000 particles at 2.0 Kelvin
billiards2.txt
cue ball striking pyramid of 3 balls
billiards4.txt
cue ball striking pyramid of 10 balls
billiards5.txt
cue ball striking pyramid of 15 balls
diffusion.txt
diffusion of particles from one side of slit
diffusion2.txt
diffusion of particles from one quarter
diffusion3.txt
brownian.txt
brownian2.txt
squeeze.txt
one tiny particle sandwiched between two big particles
squeeze2.txt
one tiny particle sandwiched between two big particles
pendulum.txt
pendulum effect
Other potential data files
Exercises
Creative Exercises


