1.5 Case Study: Union-Find
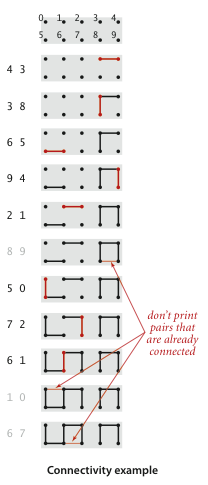
Dynamic connectivity.
The input is a sequence of pairs of integers, where each integer represents an object of some type and we are to interpret the pair p q as meaning p is connected to q. We assume that "is connected to" is an equivalence relation:- symmetric: If p is connected to q, then q is connected to p.
- transitive: If p is connected to q and q is connected to r, then p is connected to r.
- reflexive: p is connected to p.
Our goal is to write a program to filter out extraneous pairs from the sequence: When the program reads a pair p q from the input, it should write the pair to the output only if the pairs it has seen to that point do not imply that p is connected to q. If the previous pairs do imply that p is connected to q, then the program should ignore the pair p q and proceed to read in the next pair.
Union-Find API.
The following API encapsulates the basic operations that we need.

To test the utility of the API, the main() in
UF.java solves
the dynamic connectivity problem.
We also prepare test data: the file tinyUF.txt
contains the 11 connections used in our small example,
the file mediumUF.txt contains 900 connections,
and the file largeUF.txt
is an example with millions of connections.
Implementations.
We now consider several different implementations, all based on using a site-indexed array id[] to determine whether two sites are in the same component.- Quick-find.
QuickFindUF.java
maintains the invariant that p and q
are connected if and only if id[p] is equal to id[q].
In other words, all sites in a component must have the same value in
id[].

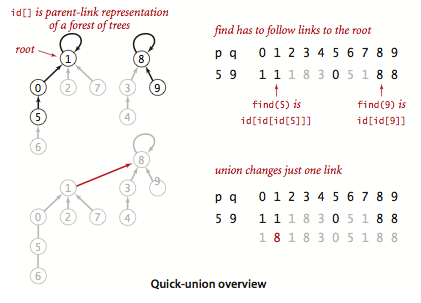
- Quick-union.
QuickUnionUF.java
is based on the same data structure—the site-indexed id[] array—but
it uses a different interpretation of the values that leads to more complicated structures.
Specifically, the id[] entry for each site will be the name of another site in the same
component (possibly itself). To implement find()
we start at the given site, follow its link to another site, follow
that sites link to yet another site, and so forth, following links until reaching a root, a
site that has a link to itself. Two sites
are in the same component if and only if this process leads them to the same root.
To validate this process, we need union() to maintain this invariant,
which is easily arranged: we follow links to find the roots associated with each of
the given sites, then rename one of the components by linking one of these
roots to the other.
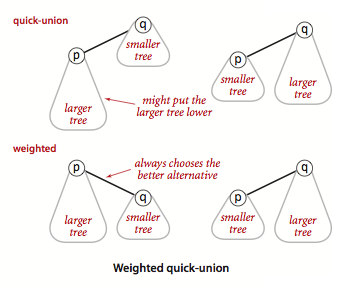
- Weighted quick-union.
Rather than arbitrarily connecting the second tree to
the first for union() in the quick-union algorithm,
we keep track of the size of each tree and always connect
the smaller tree to the larger.
Program WeightedQuickUnionUF.java
implements this approach.
- Weighted quick-union with path compression. There are a number of easy ways to improve the weighted quick-union algorithm further. Ideally, we would like every node to link directly to the root of its tree, but we do not want to pay the price of changing a large number of links. We can approach the ideal simply by making all the nodes that we do examine directly link to the root.
Union-find cost model.
When studying algorithms for union-find, we count the number of array accesses (number of times an array entry is accessed, for read or write).Definitions.
The size of a tree is its number of nodes. The depth of a node in a tree is the number of links on the path from it to the root. The height of a tree is the maximum depth among its nodes.Proposition.
The quick-find algorithm uses one array access for each call to find() and between n + 3 and 2n + 1 array accesses for each call to union() that combines two components.Proposition.
The number of array accesses used by find() in quick-union is 1 plus twice the depth of the node corresponding to the given site. The number of array accesses used by union() and connected() is the cost of the two find() operations (plus 1 for union() if the given sites are in different trees).Proposition.
The depth of any node in a forest built by weighted quick-union for n sites is at most lg n.Corollary.
For weighted quick-union with n sites, the worst-case order of growth of the cost of find(), connected(), and union() is log n.
Q + A
Q. Is there an efficient data structure that supports both insertion and deletion of edges?
A. Yes. However, the best-known fully dynamic data structure for graph connectivity is substantially more complicated than the incremental version we consider. Moreover, it's not as efficient. See Near-optimal fully-dynamic graph connectivity by Mikkel Thorup.
Exercises
- Develop classes QuickUnionUF.java and QuickFindUF.java that implement quick-union and quick-find, respectively.
-
Give a counterexample that shows why this intuitive implementation of
union() for quick-find is not correct:
public void union(int p, int q) { if (connected(p, q)) return; for (int i = 0; i < id.length; i++) if (id[i] == id[p]) id[i] = id[q]; count--; }Answer. The value of id[p] changes to id[q] in the for loop. Thus, any object r > p with id[r] equal to id[p] will not be updated to equal id[q].
- In the weighted quick-union implementation, suppose
we set id[root(p)] to q instead of id[root(q)].
Would the resulting algorithm be correct?
Answer. Yes. However, it would be increase the tree height, so the performance guarantee would be invalid.
Creative Problems
- Quick-union with path compression.
Modify QuickUnionUF.java
to include path compression, by adding a loop to find()
that links every sie on the path from p to the root.
Give a sequence of input pairs that causes this method to produce
a path of length 4. Note: the amortized cost per operation
for this algorithm is known to be logarithmic.
Solution. QuickUnionPathCompressionUF.java.
- Weighted quick-union with path compression.
Modify WeightedQuickUnionUF.java
to implement path compression, as described in Exercise 1.5.12.
Give a sequence of input pairs that causes this method to produce a tree of height 4.
Note: The amortized cost per operation for this algorithm is known to be bounded by a function known as the inverse Ackermann function and is less than 5 for any conceivable value of n that arises in practice.
Solution. WeightedQuickUnionPathCompressionUF.java.
- Weighted quick-union by height.
Develop a implementation
WeightedQuickUnionByHeightUF.java
that uses the same basic strategy as weighted quick-union but keeps track of
tree height and always links the shorter tree to the taller one.
Prove a logarithmic upper bound on the height of the trees for n
sites with your algorithm.
Solution. A union operation between elements in different trees either leaves the height unchanged (if the two tree have different heights) or increase the height by one (if the two tree are the same height). You can prove by induction that that the size of the tree is at least 2^height. Therefore, the height can increase at most lg n times.
- Random connections. Develop a UF client ErdosRenyi.java that takes an integer command-line argument n, generates random pairs of integers between 0 and n, calling connected() to determine if they are connected and then union() if not (as in our development client), looping until all sites are connected, and printing the number of connections generated. Package your program as a static method count() that takes n as argument and returns the number of connections and a main() that takes n from the command line, calls count(), and prints the returned value.
Web Exercises
- True or false. In the quick union implementation, suppose
we set parent[p] to parent[root(q)] instead of setting
parent[root(p)] to parent[root(q)].
Would the resulting algorithm be correct?
Answer. No.
-
Which of the following arrays could not possibly occur during
the execution of weighted quick union with path compression:
- 0 1 2 3 4 5 6 7 8 9
- 7 3 8 3 4 5 6 8 8 1
- 6 3 8 0 4 5 6 9 8 1
- 0 0 0 0 0 0 0 0 0 0
- 9 6 2 6 1 4 5 8 8 9
- 9 8 7 6 5 4 3 2 1 0
Solution. B, C, E, and F.
- Recursive path compression.
Implement path compression using recursion.
Solution:
public int find(int p) { if (p != parent[p]) parent[p] = find(parent[p]); return parent[p]; - Path halving. Write a data type QuickUnionPathHalvingUF.java that implements a simpler strategy known as path halving, which makes every other node on the find path link to its grandparent. Remark: the amortized cost per operation for this algorithm is known to be bounded by a function known as the inverse Ackermann function.
- Path splitting. Write a data type WeightedQuickUnionPathSplittingUF.java that implement an alternative strategy known as path splitting, which makes every node on the find path link to its grandparent. Remark: the amortized cost per operation for this algorithm is known to be bounded by a function known as the inverse Ackermann function.
- Random quick union. Implement the following version of quick union: Assign the integers 0 through n-1 uniformly at random to the n elements. When linking two roots, always link the root with the smaller label into the root with the larger label. Add in path compression. Remark: the expected cost per operation for the version without path compression is logarithmic; the expected amortized cost per operation for the version with path compression is bounded by a function known as the inverse Ackermann function.
- 3D site percolation. Repeat for 3D lattice. Threshold around 0.3117.
- Bond percolation. Same as site percolation, but choose edges at random instead of sites. True threshold is exactly 0.5.
- Given a set of N elements, create a sequence of N union operations so that weighted quick union has height Theta(log N). Repeat for weighted quick union with path compression.
- Hex. The game of Hex is played on a trapezoidal grid of hexagons.... Describe how to detect when white or black has won the game. Use the union-find data structure.
- Hex. Prove that the game cannot end in a tie. Hint: consider the set of cells reachable from the left side of the board.
- Hex. Prove that the first player can guarantee a win with perfect play. Hint: if the second player had a winning strategy, you could choose a random cell initially, and then just copy the second player's winning strategy. This is called strategy stealing.
- Labeling clusters on a grid. Physicists refer to it as the Hoshen–Kopelman algorithm although it is simply union–find on a grid graph with raster-scan order. Applications include modeling percolation and electrical conductance. Plot site occupancy probability vs. number of clusters (say 100-by-100, with p between 0 and 1, number of clusters between 0 and 1500) or distribution of clusters. (seems like DFS would suffice here) Matlab has a function bwlabel in the image processing toolbox that performs cluster labeling.


