2.2 Mergesort
The algorithms that we consider in this section is based on a simple
operation known as merging:
combining two ordered arrays to make one larger ordered array.
This operation immediately lends itself to a simple recursive sort method
known as mergesort: to sort an array,
divide it into two halves, sort the two halves (recursively),
and then merge the results.

Abstract in-place merge.
The method merge(a, lo, mid, hi) in Merge.java puts the results of merging the subarrays a[lo..mid] with a[mid+1..hi] into a single ordered array, leaving the result in a[lo..hi]. While it would be desirable to implement this method without using a significant amount of extra space, such solutions are remarkably complicated. Instead, merge() copies everything to an auxiliary array and then merges back to the original.
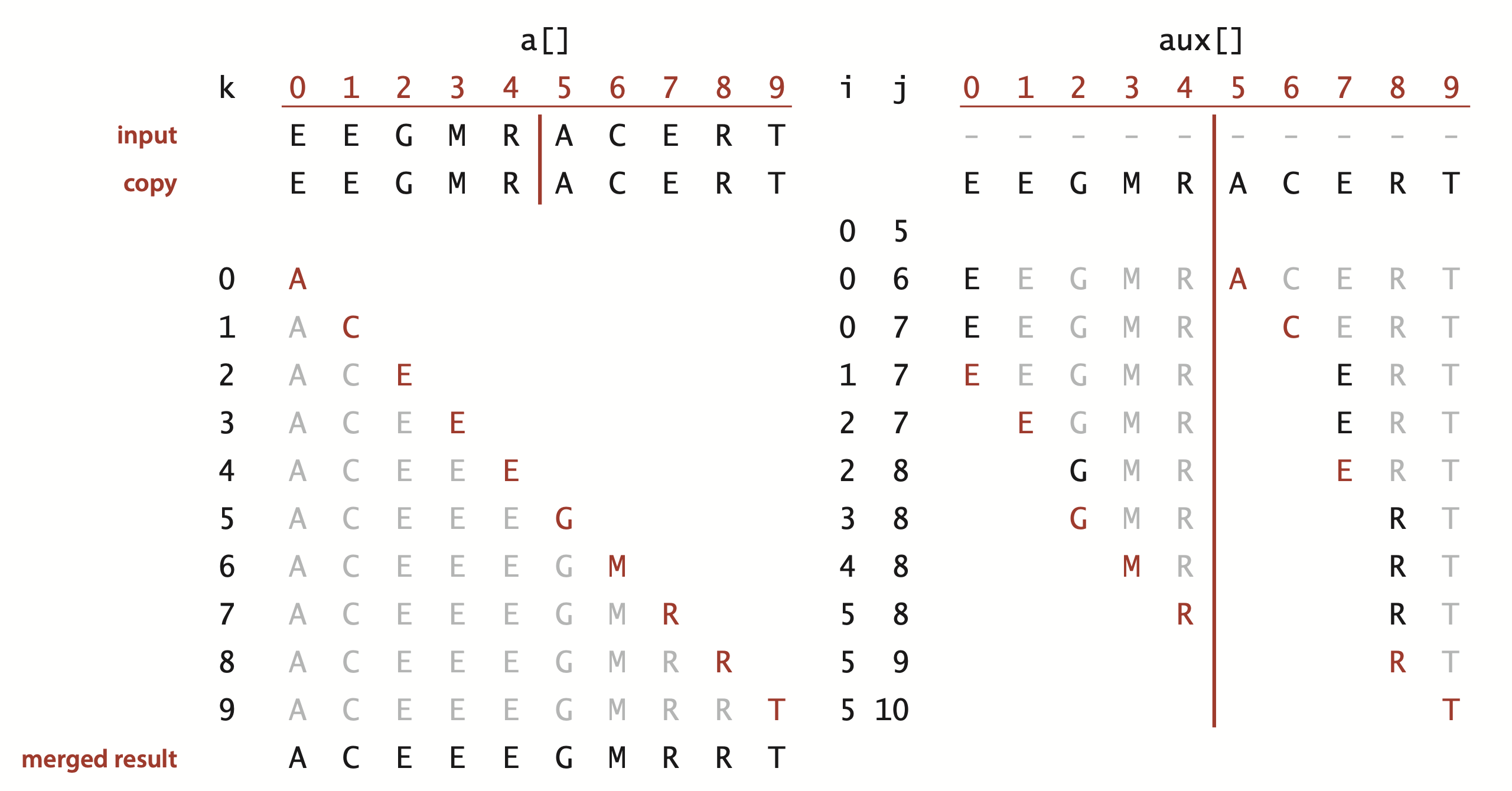
Top-down mergesort.
Merge.java is a recursive mergesort implementation based on this abstract in-place merge. It is one of the best-known examples of the utility of the divide-and-conquer paradigm for efficient algorithm design.

Proposition.
Top-down mergesort uses between 1/2 N lg N and N lg N compares and at most 6 N lg N array accesses to sort any array of length N.Improvements.
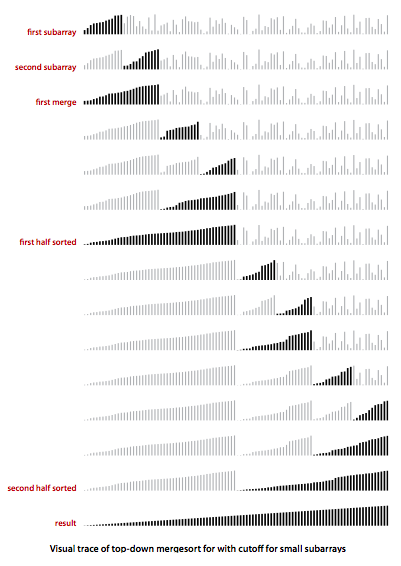
We can cut the running time of mergesort substantially with some carefully considered modifications to the implementation.- Use insertion sort for small subarrays. We can improve most recursive algorithms by handling small cases differently. Switching to insertion sort for small subarrays will improve the running time of a typical mergesort implementation by 10 to 15 percent.
- Test whether array is already in order. We can reduce the running time to be linear for arrays that are already in order by adding a test to skip call to merge() if a[mid] is less than or equal to a[mid+1]. With this change, we still do all the recursive calls, but the running time for any sorted subarray is linear.
- Eliminate the copy to the auxiliary array. It is possible to eliminate the time (but not the space) taken to copy to the auxiliary array used for merging. To do so, we use two invocations of the sort method, one that takes its input from the given array and puts the sorted output in the auxiliary array; the other takes its input from the auxiliary array and puts the sorted output in the given array. With this approach, in a bit of mindbending recursive trickery, we can arrange the recursive calls such that the computation switches the roles of the input array and the auxiliary array at each level.
Visualization.
MergeBars.java provides a visualization of mergesort with cutoff for small subarrays.
Bottom-up mergesort.
Even though we are thinking in terms of merging together two large subarrays, the fact is that most merges are merging together tiny subarrays. Another way to implement mergesort is to organize the merges so that we do all the merges of tiny arrays on one pass, then do a second pass to merge those arrays in pairs, and so forth, continuing until we do a merge that encompasses the whole array. This method requires even less code than the standard recursive implementation. We start by doing a pass of 1-by-1 merges (considering individual items as subarrays of size 1), then a pass of 2-by-2 merges (merge subarrays of size 2 to make subarrays of size 4), then 4-by-4 merges, and so forth. MergeBU.java is an implementation of bottom-up mergesort.

Proposition.
Bottom-up mergesort uses between 1/2 N lg N and N lg N compares and at most 6 N lg N array accesses to sort any array of length N.Proposition.
No compare-based sorting algorithm can guarantee to sort N items with fewer than lg(N!) ~ N lg N compares.Proposition.
Mergesort is an asymptotically optimal compare-based sorting algorithm. That is, both the number of compares used by mergesort in the worst case and the minimum number of compares that any compare-based sorting algorithm can guarantee are ~N lg N.
Exercises
-
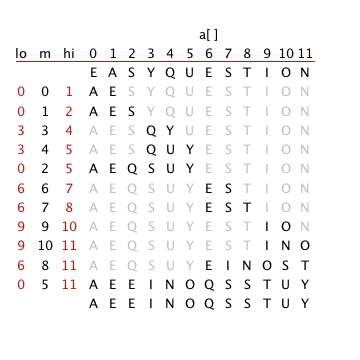
Give traces, in the style of the trace given in this section, showing how the
keys E A S Y Q U E S T I O N are sorted with top-down mergesort
and with bottom-up mergesort.
Solution.
-
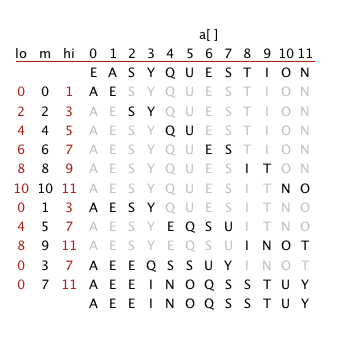
Answer Exercise 2.2.2 for bottom-up mergesort.
Solution.
-
Does the abstract inplace merge produce proper output if and only if the two
input subarrays are in sorted order? Prove your answer, or provide a counterexample.
Solution. Yes. If the subarrays are in sorted order, then the inplace merge produces proper output. If one subarray is not in sorted order, then its entries will appear in the output in the same order that they appear in the input (with entries from the other subarray intermixed).
-
Give the sequence of subarray sizes after
each merge performed by both the top-down
and the bottom-up mergesort algorithms, for n = 39.
Solution.
- Top-down mergesort: 2, 3, 2, 5, 2, 3, 2, 5, 10, 2, 3, 2, 5, 2, 3, 2, 5, 10, 20, 2, 3, 2, 5, 2, 3, 2, 5, 10, 2, 3, 2, 5, 2, 2, 4, 9, 19, 39.
- Bottom-up mergesort: 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 4, 4, 4, 4, 4, 4, 4, 4, 3, 8, 8, 8, 8, 7, 16, 16, 32, 39.
-
Suppose that top-down mergesort is modified to skip the call on merge()
whenever a[mid] <= a[mid+1].
Prove that the number of compares used for an array in sorted order is linear.
Solution. Since the array is already sorted, there will be no calls to merge(). When N is a power of 2, the number of compares will satisfy the recurrence T(N) = 2 T(N/2) + 1, with T(1) = 0.
- Use of a static array like aux[] is inadvisable in library software because multiple clients might use the class concurrently. Give an implementation of Merge.java that does not use a static array.
Creative Problems
- Faster merge.
Implement a version of merge() that copies the
second half of a[] to aux[] in
decreasing order and then does the merge back to a[].
This change allows you to remove the code to test that each of the halves
has been exhausted from the inner loop.
Note: the resulting sort is not stable.
private static void merge(Comparable[] a, int lo, int mid, int hi) { for (int i = lo; i <= mid; i++) aux[i] = a[i]; for (int j = mid+1; j <= hi; j++) aux[j] = a[hi-j+mid+1]; int i = lo, j = hi; for (int k = lo; k <= hi; k++) if (less(aux[j], aux[i])) a[k] = aux[j--]; else a[k] = aux[i++]; } - Improvements. Write a program MergeX.java that implements the three improvements to mergesort that are described in the text: add a cutoff from small subarrays, test whether the array is already in order, and avoid the copy by switching arguments in the recursive code.
- Inversions. Develop and implement a linearithmic algorithm Inversions.java for computing the number of inversions in a given array (the number of exchanges that would be performed by insertion sort for that array—see Section 2.1). This quantity is related to the Kendall tau distance; see Section 2.5.
- Index sort. Develop a version of Merge.java that does not rearrange the array, but returns an int[] perm such that perm[i] is the index of the ith smallest entry in the array.
Experiments
Web Exercises
- Merge with at most log N compares per item. Design a merging algorithm such that each item is compared at most a logarithmic number of times. (In the standard merging algorithm, an item can be compared N/2 times when merging two subarrays of size N/2.)
- Lower bound for sorting a Young tableaux.
A Young tableaux is an N-by-N matrix such that the entries are sorted
both column wise and row wise.
Prove that Theta(N^2 log N) compares are necessary to sort the N^2 entries
(where you can access the data only through the pairwise comparisons).
Solution sketch. If entry (i, j) is within 1/2 of i + j, then all of the 2N-1 grid diagonals are independent of one another. Sorting the diagonals takes N^2 log N compares.
-
Given an array a of size 2N with N items in sorted order
in positions 0 through N-1, and an array b of size
N with N items in ascending order, merge the array b
into a so that a contains all of the items
in ascending order. Use O(1) extra memory.
Hint: merge from right to left.
- k-near-sorting.
Suppose you have an array a[] of N distinct items which is nearly sorted:
each item at most k positions away from its position in the sorted order.
Design an algorithm to sort the array in time proportional to N log k.
Hint: First, sort the subarray from 0 to 2k; the smallest k items will be in their correct position. Next, sort the subarray from k to 3k; the smallest 2k items will now be in their correct position.
- Find a family of inputs for which mergesort makes strictly fewer than 1/2 N lg N
compares to sort an array of N distinct keys.
Solution: a reverse-sorted array of N = 2^k + 1 keys uses approximately 1/2 N lg N - (k/2 - 1) compares.
- Worst-case input array. Write a program MergeWorstCase.java that takes a command-line argument n and creates an input array of length n for which mergesort makes the maximum number of compares.
- Write a program SecureShuffle.java to read in a sequence of string from standard input and securely shuffle them. Use the following algorithm: associate each card with a random real number between 0 and 1. Sort the values based on their associated real numbers. Use java.security.SecureRandom to generate the random real numbers. Use Merge.indexSort() to get the random permutation.
- Merging two arrays of different lengths.
Given two sorted arrays a[] and b[] of sizes M and N where M ≥ N,
devise an algorithm to merge them into a new sorted array c[] using
~ N lg M compares.
Hint: use binary search.
Note: there is a lower bound of Omega(N log (1 + M/N)) compares. This follows because there are M+N choose N possible merged outcomes. A decision tree argument shows that this requires at least lg (M+N choose N) compares. We note that n choose r >= (n/r)^r.
- Merging three arrays. Given three sorted arrays a[], b[], and c[], each of size N, design an algorithm to merge them into a new sorted array d[] using at most ~ 6 N compares in the worst case (or, even better, ~ 5 N compares).
- Merging three arrays. Given three sorted arrays a[], b[], and c[], each of size N, prove that no compare-based algorithm can merge them into a new sorted array d[] using fewer than ~ 4.754887503 N compares in the worst case.
- Arrays with N^(3/2) inversions.
Prove that any compare-based algorithms that can sort arrays with
N^(3/2) or fewer inversions must make ~ 1/2 N lg N compares in the worst case.
Proof sketch: divide up the array into sqrt(N) consecutive subarrays of sqrt(N) items each, such that the there are no inversion between items in different subarrays but the order of items within each subarray is arbitrary. Such an array has at most N^(3/2) inversions—at most ~N/2 inversions in each of the sqrt(N) subarrays. By the sorting lower bound, it takes ~ sqrt(N) lg sqrt(N) compares to sort each subarray, for a total of ~ 1/2 N lg N.
- Optimal nonoblivious sorting.
Design algorithms that uses the fewest number of compares (in the worst case)
to sort arrays of length 3, 4, 5, 6, 7, and 8.
Solution. It is known that the optimal solution uses 3, 5, 7, 10, 13, and 16 compares, respectively. The Ford-Johnson merge insertion algorithm is known to be optimal for n <= 13. It makes sum(ceil(log[2](3*k/4)), k=1..n) compares in the worst case.


