1.4 Analysis of Algorithms
As people gain experience using computers,
they use them to solve difficult problems or to process large
amounts of data and are invariably led to questions like these:
- How long will my program take?
- Why does my program run out of memory?
Scientific method.
The very same approach that scientists use to understand the natural world is effective for studying the running time of programs:- Observe some feature of the natural world, generally with precise measurements.
- Hypothesize a model that is consistent with the observations.
- Predict events using the hypothesis.
- Verify the predictions by making further observations.
- Validate by repeating until the hypothesis and observations agree.
Observations.
Our first challenge is to determine how to make quantitative measurements of the running time of our programs. Stopwatch.java is a data type that measures the elapsed running time of a program.

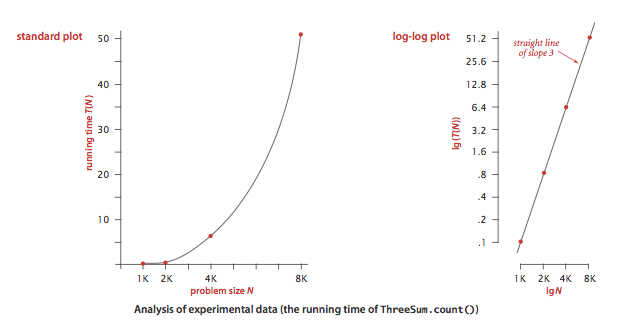
Mathematical models.
The total running time of a program is determined by two primary factors: the cost of executing each statement and the frequency of execution of each statement.- Tilde approximations.
We use tilde approximations, where we throw away
low-order terms that complicate formulas.
We write ~ f(N) to represent any function that when divided
by f(N) approaches 1 as N grows.
We write g(N) ~ f(N) to indicate that
g(N) / f(N) approaches 1 as N grows.
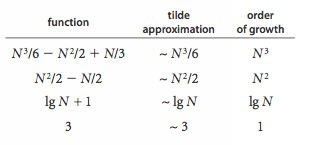
- Order-of-growth classifications.
Most often, we work with tilde approximations of the form
g(N) ~ a f(N) where f(N) = N^b log^c N
and refer to f(N) as the The order of growth
of g(N).
We use just a few structural primitives (statements, conditionals, loops,
nesting, and method calls) to implement algorithms, so very often the
order of growth of the cost is one of just a few functions of the problem
size N.

- Cost model. We focus attention on properties of algorithms by articulating a cost model that defines the basic operations. For example, an appropriate cost model for the 3-sum problem is the number of times we access an array entry, for read or write.
Property. The order of growth of the running time of ThreeSum.java is N^3.
Proposition. The brute-force 3-sum algorithm uses ~ N^3 / 2 array accesses to compute the number of triples that sum to 0 among N numbers.
Designing faster algorithms.
One of the primary reasons to study the order of growth of a program is to help design a faster algorithm to solve the same problem. Using mergesort and binary search, we develop faster algorithms for the 2-sum and 3-sum problems.- 2-sum. The brute-force solution TwoSum.java takes time proportional to N^2. TwoSumFast.java solves the 2-sum problem in time proportional to N log N time.
- 3-sum. ThreeSumFast.java solves the 3-sum problem in time proportional to N^2 log N time.
Coping with dependence on inputs.
For many problems, the running time can vary widely depending on the input.- Input models. We can carefully model the kind of input to be processed. This approach is challenging because the model may be unrealistic.
- Worst-case performance guarantees. Running time of a program is less than a certain bound (as a function of the input size), no matter what the input. Such a conservative approach might be appropriate for the software that runs a nuclear reactor or a pacemaker or the brakes in your car.
- Randomized algorithms. One way to provide a performance guarantee is to introduce randomness, e.g., quicksort and hashing. Every time you run the algorithm, it will take a different amount of time. These guarantees are not absolute, but the chance that they are invalid is less than the chance your computer will be struck by lightning. Thus, such guarantees are as useful in practice as worst-case guarantees.
- Amortized analysis. For many applications, the algorithm input might be not just data, but the sequence of operations performed by the client. Amortized analysis provides a worst-case performance guarantee on a sequence of operations.
Proposition. In the linked-list implementation of Bag, Stack, and Queue, all operations take constant time in the worst case.
Proposition. In the resizing-array implementation of Bag, Stack, and Queue, starting from an empty data structure, any sequence of N operations takes time proportional to N in the worst case (amortized constant time per operation).
Memory usage.
To estimate how much memory our program uses, we can count up the number of variables and weight them by the number of bytes according to their type. For a typical 64-bit machine,- Primitive types.
the following table gives the memory requirements for
primitive types.

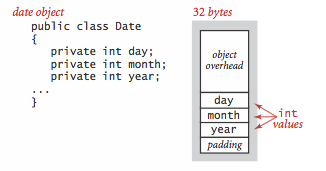
- Objects.
To determine the memory usage of an object, we add the amount of
memory used by each instance variable to the overhead associated
with each object, typically 16 bytes.
Moreover, the memory usage is typically padded
to be a multiple of 8 bytes (on a 64-bit machine).

- References. A reference to an object typically is a memory address and thus uses 8 bytes of memory (on a 64-bit machine).
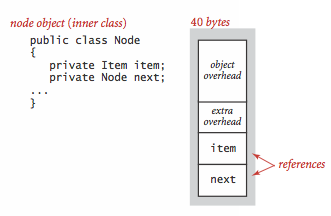
- Linked lists.
A nested non-static (inner) class such as our Node
class requires an extra 8 bytes of overhead
(for a reference to the enclosing instance).
- Arrays.
Arrays in Java are implemented as objects,
typically with extra overhead for the length. An
array of primitive-type values typically requires 24 bytes of header
information (16 bytes of object overhead, 4 bytes for the length,
and 4 bytes of padding) plus the memory needed to
store the values.

- Strings.
A Java 7 string of length N typically uses 32 bytes
(for the String object) plus 24 + 2N bytes
(for the array that contains the characters) for a total of 56 + 2N bytes.

Q + A
Q. How do I increase the amount of memory and stack space that Java allocates?
A. You can increase the amount of memory allotted to Java by executing with java -Xmx200m Hello where 200m means 200 megabytes. The default setting is typically 64MB. You can increase the amount of stack space allotted to Java by executing with java -Xss200k Hello where 200k means 200 kilobytes. The default setting is typically 128KB. It's possible to increase both the amount of memory and stack space by executing with java -Xmx200m -Xss200k Hello.
Q. What is the purpose of padding?
A. Padding makes all objects take space that is a mulitple of 8 bytes. This can waste some memory but it speeds up memory access and garbage collection.
Q. I get inconsistent timing information in my computational experiments. Any advice?
A. Be sure that you computation is consuming enough CPU cycles so that you can measure it accurately. Generally, 1 second to 1 minute is reasonable. If you are using huge amounts of memory, that could be the bottleneck. Consider turning off the HotSpot compiler, using java -Xint, to ensure a more uniform testing environment. The downside is that you are no long measuring exactly what you want to measure, i.e., actual running time.
Q. Does the linked-list implementation of a stack or queue really guarantee constant time per operation if we take into account garbage collection and other runtime processes?
A. Our analysis does not account for many system effects (such as caching, garbage collection, and just-in-time compilation)—in practice, such effects are important. In particular, the default Java garbage collector achieves only a constant amortized time per operation guarantee. However, there are real-time garbage collectors that guarantee constant time per operation in the worst case. Real time Java provides extensions to Java that provide worst-case performance guarantees for various runtime processes (such as garbage collection, class loading, Just-in-time compilation, and thread scheduling).
Exercises
-
Give the order of growth (as a function of N) of the running times
of each of the following code fragments:
-
int sum = 0; for (int n = N; n > 0; n /= 2) for (int i = 0; i < n; i++) sum++; -
int sum = 0; for (int i = 1; i < N; i *= 2) for(int j = 0; j < i; j++) sum++; -
int sum = 0; for (int i = 1; i < N; i *= 2) for (int j = 0; j < N; j++) sum++;
-
Creative Problems
- 4-sum. Develop a brute-force solution FourSum.java to the 4-sum problem.
- Local minimum in an array.
Write a program that, given an array a[] of n
distinct integers, finds a local minimum: an index i
such that botha[i] < a[i-1] and a[i] < a[i+1] (assuming the neighboring
entry is in bounds).
Your program should use ~ 2 lg n compares in the worst case.
Answer: Examine the middle value a[n/2] and its two neighbors a[n/2 - 1] and a[n/2 + 1]. If a[n/2] is a local minimum, stop; otherwise search in the half with the smaller neighbor.
- Local minimum in a matrix.
Given an n-by-n array a[] of n2
distinct integers, design an algorithm that runs in time proportional to
n log n to find a local minimum:
an pair of indices i and j such that
a[i][j] < a[i+1][j],
a[i][j] < a[i][j+1],
a[i][j] < a[i-1][j], and
a[i][j] < a[i][j-1] (assuming the neighboring entry is in bounds).
Hint: Find the minimum entry in row n/2, say a[n/2][j]. If it's a local minimum, then return it. Otherwise, check it's two vertical neighbors a[n/2-1][j] and a[n/2+1][j]. Recur in the half with the smaller neighbor.
Extra credit: Design an algorithm that takes times proportional to n.
- Bitonic search.
An array is bitonic if it is comprised of an increasing
sequence of integers followed immediately by a decreasing sequence of integers.
Write a program that, given a bitonic array of n
distinct int values, determines whether a given integer is
in the array.
Your program should use ~ 3 log n compares in the worst case.
Answer: Use a version of binary search, as in BitonicMax.java, to find the maximum (in ~ 1 lg n compares); then use binary search to search in each piece (in ~ 1 lg n compares per piece).
- Binary search with only addition and subtraction.
[Mihai Patrascu]
Write a program that, given an array of n distinct
integers in ascending order, determines
whether a given integer is in the array.
You may use only additions and subtractions and a
constant amount of extra memory.
The running time of your program should be proportional to
log n in the worst case.
Answer: Instead of searching based on powers of two (binary search), use Fibonacci numbers (which also grow exponentially). Maintain the current search range to be [i, i + F(k)] and keep F(k), F(k-1) in two variables. At each step compute F(k-2) via subtraction, check element i + F(k-2), and update the range to either [i, i + F(k-2)] or [i + F(k-2), i + F(k-2) + F(k-1)].
- Binary search with duplicates. Modify binary search so that it always returns the smallest (largest) index of a key of an item matching the search key.
- Throwing eggs from a building. Suppose that you have an N-story building and plenty of eggs. Suppose also that an egg is broken if it is thrown off floor F or higher, and unbroken otherwise. First, devise a strategy to determine the value of F such that the number of broken eggs is ~ lg N when using ~ lg N throws, then find a way to reduce the cost to ~ 2 lg F when N is much larger than F.
- Throwing two eggs from a building.
Consider the previous question, but now suppose you only have two eggs,
and your cost model is the number of throws. Devise a strategy to
determine F such that the number of throws is at most
2 sqrt(√ N), then find a way to reduce the cost to
~c √ F for some constant c.
Solution to Part 1: To achieve 2 * sqrt(N), drop eggs at floors sqrt(N), 2 * sqrt(N), 3 * sqrt(N), ..., sqrt(N) * sqrt(N). (For simplicity, we assume here that sqrt(N) is an integer.) Let assume that the egg broke at level k * sqrt(N). With the second egg you should then perform a linear search in the interval (k-1) * sqrt(N) to k * sqrt(N). In total you will be able to find the floor F in at most 2 * sqrt(N) trials.
- Hot or cold.
Your goal is the guess a secret integer between 1 and N.
You repeatedly guess integers between 1 and N.
After each guess you learn if it equals the secret integer (and the game
stops); otherwise (starting with the second guess), you learn if the guess is
hotter (closer to) or colder (farther from)
the secret number than your previous guess.
Design an algorithm that finds the secret number in
~ 2 lg N guesses. Then, design an algorithm that finds
the secret number in ~ 1 lg N guesses.
Hint: use binary search for the first part. For the second part, first design an algorithm that solves the problem in ~1 lg N guesses assuming you are permitted to guess integers in the range -N to 2N.
Web Exercises
- Let f be a monotonically increasing function with f(0) < 0 and f(N) > 0. Find the smallest integer i such that f(i) > 0. Devise an algorithm that makes O(log N) calls to f().
- Floor and ceiling. Given a set of comparable elements, the ceiling of x is the smallest element in the set greater than or equal to x, and the floor is the largest element less than or equal to x. Suppose you have an array of N items in ascending order. Give an O(log N) algorithm to find the floor and ceiling of x.
- Rank with lg N two-way compares. Implement rank() so that it uses ~ 1 lg N two-way compares (instead of ~ 1 lg N 3-way compares).
- Identity. Given an array a of N distinct integers (positive or negative) in ascending order. Devise an algorithm to find an index i such that a[i] = i if such an index exists. Hint: binary search.
- Majority. Given an array of N strings. An element is a majority if it appears more than N/2 times. Devise an algorithm to identify the majority if it exists. Your algorithm should run in linearithmic time.
- Majority.
Repeat the previous exercise, but this time your algorithm should
run in linear time, and only use a constant amount of extra space.
Moreover, you may only compare elements for equality, not for
lexicographic order.
Answer: if a and b are two elements and a != b, then remove both of them; majority still remains. Use N-1 compares to find candidate for majority; use N-1 comparisons to check if candidate really is a majority.
- Second smallest. Give an algorithm to find the smallest and second smallest elements from a list of N items using the minimum number of comparisons. Answer: you can do it in ceil(N + lg(N) - 2) comparisons by building a tournament tree where each parent is the minimum of its two children. The minimum ends up at the root; the second minimum is on the path from the root to the minimum.
- Find a duplicate. Given an array of N elements in which each element is an integer between 1 and N, write an algorithm to determine if there are any duplicates. Your algorithm should run in linear time and use O(1) extra space. Hint: you may destroy the array.
- Find a duplicate. Given an array of N+1 elements in which each element is an integer between 1 and N, write an algorithm to find a duplicate. Your algorithm should run in linear time, use O(1) extra space, and may not modify the original array. Hint: pointer doubling.
- Finding common elements. Given two arrays of N 64-bit integers, design an algorithm to print out all elements that appear in both lists. The output should be in sorted order. Your algorithm should run in N log N. Hint: mergesort, mergesort, merge. Remark: not possible to do better than N log N in comparison based model.
- Finding common elements. Repeat the above exercise but assume the first array has M integers and the second has N integers where M is much less than N. Give an algorithm that runs in N log M time. Hint: sort and binary search.
- Anagrams. Design a O(N log N) algorithm to read in a list of words and print out all anagrams. For example, the strings "comedian" and "demoniac" are anagrams of each other. Assume there are N words and each word contains at most 20 letters. Designing a O(N^2) algorithms should not be too difficult, but getting it down to O(N log N) requires some cleverness.
- Search in a sorted, rotated array. Given a sorted array of n distinct integers that has been rotated an unknown number of positions, e.g., 15 36 1 7 12 13 14, write a program RotatedSortedArray.java to determine if a given integer is in the list. The order of growth of the running time of your algorithm should be log n.
- Find the jump in the array. Given an array of n integers of the form 1, 2, 3, ..., k-1, k+j, k+j+1, ..., n+j, where 1 <= k <= n and j > 0, design a logarithmic time algorithm to find the integer k. That is, the array contains the integers 1 through n, except that at some point, all remaining values are increased by j.
- Find the missing integer. An array a[] contains all of the integers from 0 to N, except 1. However, you cannot access an element with a single operation. Instead, you can call get(i, k) which returns the kth bit of a[i] or you can call swap(i, j) which swaps the ith and jth elements of a[]. Design an O(N) algorithm to find the missing integer. For simplicity, assume N is a power of 2.
- Longest row of 0s. Given an N-by-N matrix of 0s and 1s such that in each row no 0 comes before a 1, find the row with the most 0s in O(N) time.
- Monotone 2d array. Give an n-by-n array of elements such that each row is in ascending order and each column is in ascending order, devise an O(n) algorithm to determine if a given element x in the array. You may assume all elements in the n-by-n array are distinct.
- You are in the middle of a road, but there is a duststorm obscuring your view and orientation. There is a shelter in only one direction, but you cannot see anything until you are right in front of it. Devise an algorithm that is guaranteed to find the shelter. Your goal is to minimize the amount you have to walk. Hint: some kind of doubling back-and-forth strategy.
- Improve the following code fragment by as big a constant
factor as you can for large n. Profile it to determine where
is the bottleneck. Assume b[] in an integer array of
length n.
double[] a = new double[n]; for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) a[j] += Math.exp(-0.5 * (Math.pow(b[i] - b[j], 2)); - In-place permutation. Write a program Permutation.java that includes functions that take an array and a permutation (or inverse permutation) and rearranges the elements in the array according to the permutation (or inverse permutation). Do it in-place: use only a constant amount of extra memory.
- Sum of three.
Given three sets A, B, and C of at most N integers each, determine
whether there exists a triple a in A, b in B, and c in C such that a + b + c = 0.
Answer: Sort B in increasing order; sort C in decreasing order; for each a in A, scan B and C for a pair that sums to -a (when the sum is too small, advance in B, when the sum is too large, advance in C).
- SumOfTwo. Given two sets A and B of at most N integers each, determine whether the sum of any two distinct integers in A equals an integer in B.
- Contiguous sum.
Given a list of real numbers and a target value V, find a contiguous
block (of any length) whose sum is as close to V as possible.
Brute force: compute the sum of each contiguous block by brute force. This takes O(N^3) time.
Partial sums: compute all partial sums s[i] = a[0] + a[1] + ... + a[i] so that contiguous blocks have a sum of the form s[j] - s[i]. This takes O(N^2) time.
Sort and binary search: form the partial sums as above and then sort them in ascending order. For each i, binary search for the s[j] that is as close to s[i] as possible. This takes O(N log N) time.
- Linear equation with 3 variables. For some fixed linear equation in 3 variables (say with integer coefficients), given N numbers, do any 3 of them satisfy the equation? Design a quadratic algorithm for the problem. Hint: see quadratic algorithm for 3-sum.
- Convolution 3-sum. Given N real numbers, determine whether there exists indices i and j such that a[i] + a[j] = a[i+j]. Design a quadratic algorithm for the problem. Hint: see quadratic algorithm for 3-sum.
- Find a majority item.
Given a arbitrarily long sequence of items from standard input
such that one item appears a strict majority of the time, identify
the majority item. Use only a constant amount of memory.
Solution. Maintain one integer counter and one variable to store the current champion item. Read in the next item and (i) if the item equals the champion item, increment the counter by one. (ii) else decrement the counter by one and if the counter reaches 0 replace the champion value with the current item. Upon termination, the champion value will be the majority item.
- Memory of arrays. MemoryOfArrays.java. Relies on LinearRegression.java.
- Memory of strings and substrings. MemoryOfStrings.java. Relies on LinearRegression.java and PolynomialRegression.java. Depends on whether you are using Java 6 or Java 7.
- Memory of a stack and queue.
What is the memory usage of a stack of N items as a function of N?
Solution. 32 + 40N (not including memory for referenced objects). MemoryOfStacks.java.
- Analysis of Euclid's algorithm.
Prove that Euclid's algorithm takes at most time proportional to N,
where N is the number of bits in the larger input.
Answer: First we assume that p > q. If not, then the first recursive call effectively swaps p and q. Now, we argue that p decreases by a factor of 2 after at most 2 recursive calls. To see this, there are two cases to consider. If q ≤ p / 2, then the next recursive call will have p' = q ≤ p / 2 so p decreases by at least a factor of 2 after only one recursive call. Otherwise, if p / 2 < q < p, then q' = p % q = p - q < p / 2 so p'' = q' < p / 2 and p will decrease by a factor of 2 or more after two iterations. Thus if p has N bits, then after at most 2N recursive calls, Euclid's algorithm will reach the base case. Therefore, the total number of steps is proportional to N.
- Find the duplicate.
Given a sorted array of N+2 integers between 0 and N with exactly one duplicate,
design a logarithmic time algorithm to find the duplicate.
Hint binary search.
-
Given an array a[] of n real numbers, design a linear-time algorithm
to find the maximum value of a[j] - a[i] where j ≥ i.
Solution:
double best = 0.0; double min = a[0]; for (int i = 0; i < n; i++) { min = Math.min(a[i], min); best = Math.max(a[i] - min, best); } -
Given an array a[] of n real numbers, design a linear-time algorithm
to find the maximum value of |a[j] - a[i]| + |j - i|.
Hint: create two arrays b[] and c[] of length n, with b[i] = a[i] - i and c[i] = a[i] + i.


