6.6 Intractability

This section under construction. The goal of complexity theory is to understand the nature of efficient computation. We have learned about analysis of algorithms, which enables us to classify algorithms according to the amount of resources they will consume. In this section, we will learn about a rich class of problems for which nobody has been able to devise an efficient algorithm.

Computational complexity.

As digital computers were developed in the 1940s and 1950s, the Turing machine served as the theoretical model of computation. In the 1960s Hartmanis and Stearns proposed measuring the time and memory needed by a computer as a function of the input size. They defined complexity classes in terms of Turing machines and proved that some problems have "an inherent complexity that cannot be circumvented by clever programming." They also proved a formal version (time hierarchy theorem) of the intuitive idea that if given more time or space, Turing machines can compute more things. In other words, no matter how hard a problem is (time and space requirements), there are always harder problems.

Computational complexity is the art and science of determining resource requirements for different problems. Computational complexity deals with assertions about any conceivable algorithm for a problem. Making such statements is significantly more challenging than understanding the running time of one particular algorithm for the problem since we must reason about all possible algorithms (even those not yet discovered). This makes computational complexity an exciting, yet daunting, field of study. We will survey some of its most important ideas and practical outgrowths.

Polynomial time.

We have analyzed the running time of an algorithm as a function of its input size. When solving a given problem, we prefer an algorithm that takes 8 N log N steps to one that takes 3 N² steps, since when N is large, the first algorithm is significantly faster than the first. The second algorithm will ultimately solve the same problem (but it might take hours instead of seconds). In contrast, an exponential time algorithm has a different qualitative behavior. For example, a brute force algorithm for the TSP might take N! steps. Even if each electron in the universe (10⁷⁹) had the power of today's fastest supercomputer (10¹² instructions per second), and each worked for the life of the universe (10¹⁷ seconds) on solving the problem, it would barely make a dent in solving a problem with N = 1,000 since 1000! >> 10¹⁰⁰⁰ >> 10⁷⁹ * 10¹² * 10¹⁷. Exponential growth dwarfs technological change. We refer to any algorithm whose running time is bounded by a polynomial in the input size (e.g., N log N or N^2) as a polynomial-time algorithm. We say that a problem is intractable if there is no polynomial-time algorithm for the problem.

Create log-log scale plot of N, N³, N⁵, N¹⁰, 1.1^N, 2^N, N! as in Harel p. 74.

As programmers gained more experience with computation, it became evident that polynomial-time algorithms were useful and exponential-time algorithms were not. In a very influential paper, Jack Edmonds referred to polynomial algorithms as "good algorithms" and argued that polynomial time is a good surrogate for efficient computation. Kurt Godel wrote a letter to von Neumann (p. 9) in 1956 that contains the (implicit) notion that polynomiality is a desirable feature. Earlier (1953), von Neumann recognized the qualitative difference between polynomial and exponential algorithms. The idea of classifying problems according to polynomial and exponential time profoundly changed the way people thought about computational problems.

NP.

Informally we define a search problem as a computational problem where we are looking for a solution among a (potentially huge) number of possibilities, but such that when we find a solution, we can easily check that it solves our problem. Given an instance I of a search problem (some input data specifying the problem), our goal is to find a solution S (an entity that meets some pre-specified criterion) or report that no such solution exists. To be a search problem, we require that it be easy to check that S is indeed a solution. By easy, we mean polynomial-time in the size of the input I. The complexity class NP is the set of all search problems. Here are a few examples.

Linear systems of equations. Given a system of linear equations Ax = b, find a solution x that satisfies the equations (if one exists). The problem is in NP because if we are given a purported solution x, we can check that Ax = b by plugging in x and verifying each equation.
Linear programming. Given a system of linear inequalities Ax ≤ b, find a solution x that satisfies the inequalities (if one exists). The problem is in NP because if we are given a purported solution x, we can check that Ax ≤ b by plugging in x and verifying each inequality.
Integer linear programming. Given a system of linear inequalities Ax ≤ b, find a binary (0/1) solution x that satisfies the inequalities (if one exists). The problem is in NP because if we are given a purported solution x, we can check that Ax ≤ b by plugging in x and verifying each inequality.

While it is easy to check a proposed solution to all three problems, how difficult is it to find a solution from scratch?

Remark: our definition of NP is slightly non-standard. Historically, complexity classes were defined in terms of decision problems (yes-no problems). For example, given a matrix A and a vector b, does there exist a solution x such that Ax = b?

P.

The complexity class P is the set of all search problems solvable in polynomial-time (on a deterministic Turing machine). As before, we define P in terms of search problems (instead of decision problems). It captures most of the problems that we can solve in practice on real machines. We list a few examples below:

Problem	Description	Algorithm	Instance	Solution
GCD	Find the greatest common divisor of two integers x and y.	Euclid's algorithm (Euclid, 300 BCE)	34, 51	17
STCONN	Given a graph G and two vertices s and t, find a path from s to t.	BFS or DFS (Theseus)
SORT	Find permutation that puts elements in ascending order.	Mergesort (von Neumann, 1945)	2.3 8.5 1.2 9.1 2.2 0.3	5 2 4 0 1 3
PLANARITY	Given a graph G, draw it in the plane so that no two edges cross.	(Hopcroft-Tarjan, 1974)
LSOLVE	Given a matrix A and a vector b, find a vector x such Ax = b.	Gaussian elimination (Edmonds, 1967)	x+y=1 2x+4y=3	x = 1/2 y = 1/2
LP	Given a matrix A and a vector b, find a vector x such that Ax ≤ b?	Ellipsoid algorithm (Khachiyan, 1979)	x+y≤1 2x+4y≤3	x = 0 y = 0
DIOPHANTINE	Given a (sparse) polynomial of one variable with integer coefficients, find an integral root?	(Smale et. al, 1999)	x⁵ - 32	x = 2

Extended Church-Turing Thesis.

In the mid 1960s Cobham and Edmonds independently observed that the set of problems solvable in a polynomial number of steps remains invariant over a very wide range of computational models, from deterministic Turing machines to RAM machines. The extended Church-Turing thesis asserts that the Turing machine is as efficient as any physical computing device. That is, P is the set of search problems solvable in polynomial-time in this universe. If some piece of hardware solves a problem of size N in time T(N), the extended Church-Turing thesis asserts that a deterministic Turing machine can do it in time T(N)^k for some fixed constant k, where k depends on the particular problem. Andy Yao expresses the broad implications of this thesis:

They imply that at least in principle, to make future computers more efficient, one only needs to focus on improving the implementation technology of present-day computer designs.

In other words, any reasonable model of computation can be efficiently simulated on a (probabilistic) Turing machine. The extended Church-Turing thesis is true for all known physical general purpose computers. For random access machines (e.g., your PC or Mac) the constant k = 2. So, for example, if a random access machine can perform a computation in time N^3/2, then a Turing machine can do the same computation in time N³.

Does P = NP?

One of the most profound scientific questions of our time is whether P = NP. That is, can all search problems be solved in polynomial time? Clay Foundation offers a 1 million dollar millennium prize for solving it. Here are some speculations on when the question will be resolved. The overwhelming consensus is that P != NP, but nobody has been able to prove it.

Video of Homer Simpson pontificating over P = NP, with accompanying music Erased by Paradise Lost.

Godel's letter to von Neumann anticipated the P = NP question. He recognized that if P = NP (satisfiability is in P), it "would have consequences of the greatest importance" since then "the mental work of a mathematician concerning Yes-or-No questions could be completely replaced by a machine." He asked for which combinatorial problems was there a more efficient alternative to exhaustive search.

NP-completeness.

Informally, NP-complete problems are the "hardest" problems in NP; they are the ones most likely to not be in P. Define: a problem is NP-complete if (i) it is in NP and (ii) every problem in NP polynomial reduces to it. Defining the concept of NP-completeness does not mean that such problems exist. In fact, the existence of NP-complete problems is an amazing thing. We cannot prove a problem is NP-complete by presenting a reduction from each NP problem since there are infinitely many of them. In the 1960s, Cook and Levin proved that SAT is NP-complete.

This is an example of universality: if we can solve any NP-complete, then we can solve any problem in NP. Unique scientific discovery giving common explanation to all sorts of problems. It is even more amazing that there exist "natural" problems that are NP-complete.

The impact of NP-completeness on the natural sciences has been undeniable. One the first NP-complete problems were discovered, intractability "spread like a shockwave through the space of problems", first in computer science, and then to other scientific disciplines. Papadimitriou lists 20 diverse scientific disciplines that were coping with internal questions. Ultimately, scientists discovered their inherent complexity after realizing that their core problems were NP-complete. NP-completeness is mentioned as a keyword in 6,000 scientific papers per year. "Captures vast domains of computational, scientific, mathematical endeavors, and seems to roughly delimit what mathematicians and scientists had been aspiring to compute feasibly." [Papadimitriou] Few scientific theories have had such a breadth and depth of influence.

Some NP-complete problems. Since the discovery that SAT is NP-complete, tens of thousands of problems have been identified as NP-complete. In 1972, Karp showed that 21 of the most infamous problem s in discrete mathematics were NP-complete, including Tsp, Knapsack, 3Color, and Clique. The failure of scientists to find an efficient algorithm for these 21 problems, despite being unaware that they were NP-complete, was among the first evidence suggesting that P != NP. Below we list a sampling of some NP-complete problems. Here are some more NP-complete problems. This is only meant to illustrate their diversity and pervasiveness.

Bin Packing. You have n items and m bins. Item i weighs w[i] pounds. Each bin can hold at most W pounds. Can you pack all n items into the m bins without violating the given weight limit?
This problem has many industrial applications. For example, UPS may need to ship a large number of packages (items) from one distribution center to another. It wants to put them into trucks (bins), and use as few trucks as possible. Other NP-complete variants allow volume requirements: each 3-dimensional package takes up space and you also have to worry about arranging the packages within the truck.
Knapsack. You have a set of n items. Item i weighs w[i] pounds and has benefit b[i]. Can you select a subset of the items that have total weight less than or equal to W and total benefit greater than or equal to B? For example, when you go camping, you must select items to bring based on their weight and utility. Or, suppose you are burglarizing a home and can only carry W pounds of loot in your knapsack. Each item i weighs w[i] pounds has a street value of b[i] dollars. Which items should you steal?
Subset Sum. Given n integers does there exists a subset of them that sum exactly to B? For example, suppose the integers are {4, 5, 8, 13, 15, 24, 33}. If B = 36 then the answer is yes (and 4, 8, 24 is a certificate). If B = 14 the answer is no.
Partition. Given n integers, can you divide them into two subsets so that each subset sums to the same number? For example, suppose the integers are {4, 5, 8, 13, 15, 24, 33}. Then the answer is yes, and {5, 13, 33} is a certificate. Load balancing for dual processors.
Integer linear programming. Given an integer matrix A and an integer vector b, does there exist an integer vector x such that Ax ≤ b? This is a central problem in operations research since many optimization problems can be formulated in this way. Note the contrast to the linear programming problem presented above where we are looking for a rational vector instead of an integer vector. The line between problems which are tractable and problems which are intractable can be very subtle.
SAT. Given n Boolean variables x₁, x₂, ..., x_N and a logical formula, is there an assignment of truth variables that makes the formula satisfiable, i.e., true? For example, suppose the formula is
(x₁' + x₂ + x₃) (x₁ + x₂' + x₃) (x₂ + x₃) (x₁' + x₂' + x₃')
Then, the answer is yes and (x₁, x₂, x₃) = (true, true, false) is a certificate. Many applications to electronic design automation (EDA), including testing and verification, logic synthesis, FPGA routing, and path delay analysis. Application to AI, including knowledge base deduction and automatic theorem proving.
Exercise: given two circuits C1 and C2, design a new circuit C such that some setting of input values makes C output true if and only if C1 and C2 are equivalent.
3-SAT. Given n Boolean variables x₁, x₂, ..., x_N and a logical formula in conjunction normal form (product-of-sums) with exactly 3 distinct literals per clause, is there an assignment of truth variables that makes the formula satisfiable?
Clique. Given n people and a list of pairwise friendships. Is there a group or clique of k people such that every possible pair of people within the group are friends? It is convenient to draw the friendship graph, where we include a node for each person and an edge connecting each pair of friends. In the following example with n = 11 and k = 4, the answer is yes, and {2, 4, 8, 9} is a certificate.
Longest path. Given a set of nodes and pairwise distances between nodes, does there exists a simple path of length at least L connecting some pair of nodes?
Machine Scheduling. Your goal is to process n jobs on m machines. For simplicity, assume each machine can process any one job in 1 time unit. Also, there can be precedence constraints: perhaps job j must finish before job k can start. Can you schedule all of the jobs to finish in L time units?
Scheduling problems have a huge number of applications. Jobs and machines can be quite abstract: to graduate Princeton you need to take n different courses, but are unwilling to take more than m courses in any one semester. Also, many courses have prerequisites (you can't take COS 226 or 217 before taking 126, but it is fine to take 226 and 217 at the same time). Can you graduate in L semesters?
Shortest Common Superstring. Given the genetic alphabet { a, t, g, c } and N DNA fragments (e.g., ttt, atggtg, gatgg, tgat, atttg) is there a DNA sequence with K or fewer characters that contains every DNA fragment? Suppose K = 11 in the above example; then the answer is yes and atttgatggtg is a certificate. Applications to computational biology.
Protein folding. Proteins in organism fold in three dimensional dimensional space in a very specific way, to their native state. This geometric pattern determines the behavior and function of a protein. One of the most widely used folding models is the two dimensional hydrophilic-hydrophobic (H-P) model. In this model, a protein is a sequence of 0s and 1s, and the problem is to embed it into a 2-d lattice such that the number of pairs of adjacent 1s in the lattice, but not in the sequence (its energy), is minimized. For example, the sequence 011001001110010 is embedded in the figure below in such a way that there are 5 new adjacent pairs of 1s (denoted by asterisks).
0 --- 1 --- 1 --- 0 * * | 0 --- 1 --- 1 0 | * | | 0 --- 1 * 1 * 1 | | | 0 0 --- 0
Minimizing the H-P energy of a protein is NP-hard. (Papadimitriou, et al.) It is well accept by biologists that proteins fold to minimize their energies. A version of Levinthal's paradox asks how it is possible that proteins are able to efficiently solve apparently intractable problems.
Integration. Given integers a₁, a₂, ..., a_N, does the following integral equal 0?

If you see this integral in your next Physics course, you should not expect to be able to solve it. This should not come as a big surprise because in Section 7.4 we consider a version of integration that is undecidable.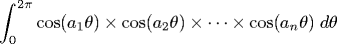
Crossword puzzle. Given an integer N, and a list of valid words, is it possible to assign letters to the cells of an N-by-N grid so that all horizontal and vertical words are valid? No easier if some of the squares are black as in a crossword puzzle.
Theorem. Given a purported theorem (such as one for the Riemann Hypothesis), can you prove it is true using at most n symbols in some formal system such as Zermelo-Fraenkel set theory?
Tetris.
Minesweeper.
Regular expressions. Give two regular expressions over the unary alphabet { 1 }, do they represent different languages? Give two NFAs, do they represent different languages? It may not be apparent that either problem is even decidable since we don't have an obvious bound on the size of the smallest string that is in one language but not the other. [Note that the corresponding inequivalence problem for DFAs is polynomial solvable.] The reason why we phrase the problem as inequivalence instead of equivalence is that it is easy to check that the two entities are non-equivalent by demonstrating a string s. In fact, if the two languages are different, then the smallest string is polynomial in the size of the input. Thus, we can use the efficient algorithms from Section 7.xyz to check whether s is recognized by an RE or accepted by an NFA. However, to argue that two REs are equivalent, we would need an argument that guarantees that all strings in one are in the other, and vice versa. [It is possible to devise an (exponential) algorithm to test whether two REs or NFAs are equivalent, although this should not be obvious.]
Lemmings. Is it possible to guide a tribe of green-haired lemming creatures to safety in a level of the game Lemmings?
Multinomial minimization over unit hypercube. Given a multinomial of N variables, is the minimum <= C, assuming all variables are bounded between 0 and 1. Classic calculus problem: min f(x) = ax^2 + bx + c over [0, 1]. Derivative at x = ?? is 0, but minimum occurs at boundary.
Quadratic Diophantine equations. Given positive integers a, b, and c, are there positive integers x and y such that ax² + by = c?
Knot theory. Which knots on a 3-dimensional manifold bound a surface of genus ≤ g?
Bounded Post Correspondence Problem. Given a post correspondence problem with N cards and an integer K &le N, is there a solution that uses at most K cards? Recall it is undecidable if there is no limit on K.
Nash equilibria. Cooperative game theory. Given a 2-player game, find a Nash equilibrium that maximizes the payoff to player 1. Do more than one NE exist? Is there a NE that is Pareto optimal? NE that maximizes social welfare.
Quadratic congruence. Given positive integers a, b, and c, is there a positive integer x < c such that x² = a (mod b)?
Ising model in 3d. Simple mathematical model of phase transitions, e.g., when water freezes or when cooling iron becomes magnetic. Computing lowest energy state is NP-hard. Solvable in polynomial time if graph is planar, but 3d lattice is nonplanar. Holy grail of statistical mechanics for 75 years before proved NP-hard. Establishing NP-completeness means that physicists won't spend another 75 years attempting to solve the unsolvable.
Bandwidth minimization. Given an N-by-N matrix A and an integer B, is it possible to permute the rows and columns of A such that A_ij = 0 if |i - j| > B. Useful for numerical linear algebra.
Voting and social choice. NP-hard for an individual to manipulate a voting scheme known as single transferable vote. NP-hard to determine who has won an election in a scheme seriously proposed by Lewis Carroll (Charles Dodgson) in 1876. In Carroll's scheme, the winner is the candidate who with the fewest pairwise adjacent changes in voters' preference rankings becomes the Condercet winner (a candidate who would beat all other candidates in a pairwise election). Shapley-Shubik voting power. Computing the Kemeny optimal aggregation.

Coping with intractability.

The theory of NP-completeness says that unless P = NP, there are some important problems for which we can't create an algorithm that simultaneously achieves the following three properties:

Guarantee to solve the problem in polynomial-time.
Guarantee to solve the problem to optimality.
Guarantee to solve arbitrary instances of the problem.

When we encounter an NP-complete problem, we must relax one of the three requirements. We will consider solutions to the TSP problem that relax one of the three goals.

Complexity theory deals with worst-case behavior. This leaves open the possibility of designing algorithms that run quickly on some instances, but take a prohibitive amount of time on others. For example, Chaff is a program that can solve many real-world SAT instances with 10,000 variables. Remarkably, it was developed by two undergraduates at Princeton. The algorithm does not guarantee to run in polynomial time, but the instances we're interested in may be "easy."

Sometimes we may be willing to sacrifice the guarantee on finding the optimal solution. Many heuristic techniques (simulating annealing, genetic algorithms, Metropolis algorithm) have been designed to find "nearly optimal" solutions to the TSP problem. Sometimes it is even possible to prove how good the resulting solution will be. For example, Sanjeev Arora designed an approximation algorithm for the Euclidean TSP problem that guarantees to find a solution that costs at most, say 1%, above the optimum. Designing approximation algorithms is an active area of research. Unfortunately, there are also non-approximability results of the form: if you can find an approximation algorithm for problem X that guarantees to get within a factor of 2 of the optimum, then P = NP. Thus, designing approximation algorithms for some NP-complete problems is not possible.

If we are trying to solve a special class of TSP problems, e.g., where the points lie on the boundary of a circle or the vertices of an M-by-N lattice, then we can design efficient (and trivial) algorithms to solve the problem.

Exploiting intractability. Having intractability problems is occasionally a good thing. In Section XYZ, we will exploit intractable problems to design cryptographic systems.

Between P and NP-complete. Most natural problems in NP are now known to be in P or NP-complete. If P != NP, then there are provably some NP problems that are neither in P or NP-complete. Like "dark matter we have not developed means of observing." A few notable unclassified problems in the netherworld: factoring, and subgraph isomorphism.

Factoring. Best known algorithm is 2^O(n^1/3 polylog(n)) - number field sieve. Believed by experts not to be in P.
Precedence constrained 3-processor scheduling. Given a set of unit length tasks, and a precedence order, find the shortest schedule on 3 parallel machines.
Turnpike problem. Given N(N-1)/2 positive numbers (not necessarily distinct), does there exist a set of N points on the line such that these numbers are the pairwise distances of the N points. Intuition: points are exits on I-95. Problem first arose in 1930s in the context of x-ray crystallography. Also known as the partial digest problem in molecular biology.
Boolean formula dualization. Given a monotone CNF formula and a monotone DNF formula, are they equivalent? (a + b)(c + d) = ac + ad + bc + bd. Naively applying De Morgan's law leads to exponential algorithm because of redundancy. Best algorithm O(n^(log n / log log n)).
Stochastic games. White, Black and Nature alternate moving a token on the edges of a directed graph, starting at the start state s. White's goal is to move the token to a goal state t. Black's goal is to prevent the token from ever reaching t. Nature moves the tokens at random. Given a digraph, a start state s, and a goal state t,, does White have a strategy which will make the token reach t with probability ≥ 1/2? Problem is in NP intersect co-NP, but not known to be in P. Believed to be in P, we just haven't found a polynomial-time algorithm.

Other complexity classes.

The complexity classes P, NP, and NP-complete are the three most famous complexity classes. Scott Aaronson's website The Complexity Zoo contains a comprehensive list of other complexity classes that are useful in classifying problems according to their computational resources (time, space, parallelizability, use of randomness, quantum computing). We describe a few of the most important ones below.

PSPACE. The complexity class PSPACE = problems solvable by a Turing machine using polynomial space. PSPACE-complete = in PSPACE and every other problem in PSPACE can be reduced to it in polynomial time.
- Here is a complexity version of the halting problem. Given a Turing machine that is limited to n tape cells, does it halt in at most k steps? The problem is PSPACE-complete, where n is encoded in unary. This means that unless P = PSPACE, we are unlikely to be able to tell whether a given program, running on a computer with n units of memory, will terminate before k steps substantially faster than the trivial method of running it for k steps and seeing what happens.
- Bodlaender: given a graph with vertices 1, ..., N, two players alternate in labeling the vertices red, green, or blue. The first player to label a vertex the same color as one of its neighbors loses. Determining whether there is a winning strategy for the first player is PSPACE-complete.
- Versions of many conventional games are provably intractable; this partially explains their appeal. Also natural generalizations of Othello, Hex, Geography, Shanghai, Rush Hour, go-moku, Instant Insanity, and Sokoban are PSPACE-complete.
  Eppstein's list of hard games.
- Is a given string a member of a context sensitive grammar?
- Do two regular expressions describe different languages? PSPACE-complete even over the binary alphabet and if one of the regular expressions is .*.
- Another example that can be made rigorous is the problem of moving a complicated object (e.g., furniture) with attachments that can move and rotate through an irregularly shaped corridor.
- Another example arises in parallel computing when the challenge is to determine whether a deadlock state is possible within a system of communicating processors.
Note PSPACE = NPSPACE (Savitch's theorem).
EXPTIME. The complexity class EXPTIME = all decision problem solvable in exponential time on deterministic Turing machine. Note P ⊆ NP ⊆ PSPACE ⊆ EXPTIME, and, by the time hierarchy theorem, at least one inclusion is strict, but unknown which one (or more). It is conjectured that all inclusions are strict.
- Roadblock from Harel p. 85.
- Natural generalization of chess, checkers, Go (with Japanese style ko termination rule), and Shogi are EXPTIME-complete. Given a board position, can the first player force a win? Here N is the size of the board, and the running time is exponential in N. One reason that these problems are harder from a theoretical standpoint than Othello (and other PSPACE-complete games) is that they can take an exponential number of moves. Checkers (aka English draughts on an N-by-N board): player can have an exponential number of moves at a given turn because of jump sequences. [pdf] Note: depending on termination rules, checkers can either be PSPACE-complete or EXPTIME-complete. For EXPTIME-complete, we assume the "forced capture rule" where a player must make a jump (or sequence of jumps) if available.
- Here is a complexity version of the halting problem. Given a Turing machine, does it halt in at most k steps? Alternatively, given a fixed Java program and a fixed input, does it terminate in at most k steps? The problem is EXPTIME-complete. Here the running time is exponential in the binary representation of k. In fact, no turing machine can guarantee to solve it in, say, O(k / log k) steps. Thus, brute force simulation is essentially best possible: provably, the problem cannot be solved substantially faster than the trivial method of running the Turing machine for the first k steps and seeing what happens.
An EXPTIME-complete problem cannot be solved in polynomial-time on a deterministic Turing machine - it does not depend on the P ≠ NP conjecture.
EXPSPACE. EXPSPACE-complete: given two "extended" regular expressions, do they represent different languages? By extended, we allow a squaring operation (two copies of an expression). Stockmeyer and Meyer (1973). Or, more simply set intersection (Hunt, 1973). Word problem for Abelian groups (Cardoza, Lipton, Meyer, 1976), Vector Addition Subsystem.
The Vector Addition Subsystem is EXPSAPCE-hard: given a nonnegative vector s and a set of arbitrary vectors, v1, v2, ..., vn, a vector x is reachable from s if it is either (i) the vector s or (ii) the vector y + vi where y is reachable. The VAS problem is to determine whether a given vector x is reachable.
DOUBLE-EXPTIME. The class DOUBLE-EXPTIME is the set of all decision problems solvable in doubly exponential time. A remarkable example is determining whether a formula in first order Presburger arithmetic is true. Presburger arithmetic consists of statements involving integers with + as the only operation (no multiplication or division). It can model statements like the following: if x and y are integer such that x &le y + 2, then y + 3 > x. In 1929 Presburger proved that his system is consistent (can't prove a contradiction like 1 > 2) and complete (every statement can be proven true or false). In 1974, Fischer and Rabin proved that any algorithm that decides the truth of a Presburger formula requires at least 2^{(2^cN)} time for some constant c, where N is the length of the formula.
Non-elementary. More than 2^2^2^...^2^N for any finite tower. Given two regular expressions that allow squaring and complementation, do they describe different languages?

Output polynomial time.

Some problems involve more output than a single bit of information. For example, outputting a solution to the Towers of Hanoi problem requires at least 2^N steps. This requirement is not because the solution is inherently hard to compute, but rather because there are 2^N symbols of output, and it takes one unit of time to write each output symbol. Perhaps a more natural way to measure efficiency is a function both of the input size and of the output size. A classic electrical engineering problem with DFAs is to build a DFA from a RE that uses the minimum number of states. We would like an algorithm that is polynomial in the size of the input RE (number of symbols) and also in the size of the output DFA (number of states). Unless P = NP, designing such an algorithm is impossible. In fact, it's not even possible to design a polynomial algorithm that gets the answer within a constant (or even polynomial) number of states! Without the theory of NP-completeness, researchers would waste time following unpromising research directions.

Other lower bounds.

Information theoretic. In Section X.Y we saw that insertion uses at most N^2 compares to sort N items, and mergesort uses at most N log N compares. A natural question to ask is whether we can do better, perhaps one that uses at most 5N compares or even 1/2 N log N compares. To make the question more precise, we must explicitly state our computational model (decision tree). Here, we assume that we only access the data through the less() function. A remarkable theorem due to X says that no (comparison based) sorting algorithm can guarantee to sort every input of N distinct elements in fewer than ~ N log N compares. To see why, observe that each compare (call to less) provides one bit of information. In order to identify the correct permutation, you need log N! bits, and log N! ~ N log N. This tells us that mergesort is (asymptotically) the best possible sorting algorithm. No sorting algorithm in existence (or even one not yet imagined) will use substantially fewer compares.
3-Sum hard. Given a set of N integers, do any three of them sum to 0? Quadratic algorithm exists (see exercise xyz), but no subquadratic algorithm known. 3-SUM linear reduces to many problems in computational geometry. (find whether set of points in the plane have 3 that are collinear, decide whether a set of line segments in the plane can be split into two subsets by a line, determining whether a set of triangles cover the unit square, can you translate a polygon P to be completely inside another polygon Q, robot motion planning).

Brute force TSP takes N! steps. Using dynamic programming, can get it down to 2^N. Best lower bound = N. Essence of computational complexity = trying to find matching upper and lower bounds.

Circuit complexity.

There are other ways to define and measure computational complexity. A Boolean circuit of n inputs can compute any Boolean function of n variables. We can associate the set of binary strings of size n for which the circuit outputs 1 as the set of strings in the language. We need one circuit for each input size n. Shannon (1949) proposed the size of the circuit as a measure of complexity. It is known that a language has uniformly polynomial circuits if and only if the language is in P.

Physical and analog computation.

The P = NP question is a mathematical question regarding the capabilities of Turing machines and classical digital computers. We might also wonder whether the same is true for analog computers. By analog, we mean any "deterministic physical device that uses a fixed number of physical variables to represent each problem variable." Internal state represented by continuous variables instead of discrete. E.g., soap bubbles, protein folding, quantum computing, gears, time travel, black holes, etc.

Vergis, Steiglitz, and Dickinson proposed an analog form of the Strong Church-Turing thesis:

Any finite analog computer can be simulated efficiently by a digital computer, in the sense that the time required by the digital computer to simulate the analog computer is bounded by a polynomial function of the resources used by the analog computer.

The resources of the analog computer could be time, volume, mass, energy, torque, or angular momentum. Reference: The Physics of Analog Computation

Any reasonable model of computation (e.g., not involving exponential parallelism) can be simulated in polynomial time by a Turing machine (supplemented by a hardware random number generator).

Reference: Scott Aaronson. Can yield new insights into physics. One day "the presumed intractability of NP-complete problems might be taken as a useful constraint in the search for new physical theories" just like the second law of thermodynamics. Still can be falsified by experiment, but don't waste time looking...

Soap bubbles. Folklore that you can solve Steiner tree problem. In reality, only finds a local minimum, and may take a while to do so.
Quantum computing. One speculative model of computation - quantum computers - might be capable of solving some problems in a polynomial time that a deterministic Turing machine cannot do. Peter Shor discovered an N^3 algorithm for factoring N-digit integers, but the best known algorithm on a classical computer takes time exponential in N. Same idea could lead to a comparable speedup in simulating quantum mechanical systems. This explains the recent excitement in quantum computation, as it could result in a paradigm shift for computing. However, quantum computers do not yet violate the extended Church-Turing thesis since we don't yet know how to build them. (Difficult to harness because much of the quantum information seems to be easily destroyed by its interactions with the outside world, i.e., decoherence.) Moreover, it is still possible that someone might discover a polynomial-time algorithm for factoring on a classical computer, although most experts suspect that this is not possible. Grover's algorithm: search in sqrt(N) time instead of N.
Richard Feynman showed in 1982 that classical computers cannot simulate quantum mechanical systems without slowing down exponentially (crux of argument is that Turing machines have locality of reference whereas quantum mechanics includes "exploit spooky action at a distance"). A quantum computer might be able to get around this problem. Feynman quote with respect to building a computer to simulate physics...
"The rule of simulation that I would like to have is that the number of computer elements required to simulate a large physical system is only to be proportional to the space-time volume of the physical system. I don't want to have an explosion."
Rephrase in terms of modern complexity theory by replacing "proportional to" by "bounded by a polynomial function of".
Deutsch-Jozsa give algorithm that is provably exponentially faster on a quantum computer than on a deterministic Turing machine. (Though exponential gap does not exist if the Turing machine has access to a hardware random number generator and can be wrong with negligible probability. Quantum computers can generate true randomness. )

PRIMES and COMPOSITE.

It is easy to convince someone that a number is composite by producing a factor. Then, the person just has to check (by long division) that you did not lie to them. Marin Mersenne conjectured that numbers of the form 2^p - 1 are prime for p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 and 257. His conjecture for p = 67 was disproved by F. N. Cole over two hundred and fifty years later in 1903. According to E. T. Bell's book Mathematics: Queen and Servant of Science

In the October meeting of the AMS, Cole announced a talk "On the Factorisation of Large Numbers". He walked up to the blackboard without saying a word, calculated by hand the value of 2⁶⁷, carefully subtracted 1. Then he multiplied two numbers (which were 193707721 and 761838257287). Both results written on the blackboard were equal. Cole silently walked back to his seat, and this is said to be the first and only talk held during an AMS meeting where the audience applauded. There were no questions. It took Cole about 3 years, each Sunday, to find this factorization, according to what he said.

For the record 2⁶⁷ - 1 = 193707721 × 761838257287 = 147573952589676412927.

Q + A

Q. Are polynomial algorithms always useful?

A. No, algorithms that take N¹⁰⁰ or 10¹⁰⁰ N² steps are as useless in practice as exponential ones. The constants that arise in practice are usually sufficiently small that polynomial-time algorithms scale to huge problems, so polynomiality often serves as a surrogate for useful in practice.

Q. Why is the class of all search problems named NP?

A. The original definition of NP was in terms of nondeterministic Turing machines: NP is the set of all decision problems that can be solved in polynomial-time on a nondeterministic Turing machine. Roughly speaking, the difference between a deterministic and nondeterministic Turing machine is that the former operates like a conventional computer, performing each instruction in sequence, forming a computational path; a nondeterministic Turing machine can "branch off" where each branch can execute a different statement in parallel, forming a computational tree (If any path in the tree leads to a YES, then we accept; if all paths lead to NO, we reject.) This is where the N in NP comes from. It turns out the two definitions are equivalent, but the certificate one is now more widely used. (Also, Karp's 1972 paper uses the polynomial-time verifiability definition.)

Q. What is the complexity class NP-hard?

A. Several competing definitions. We define a problem (decision, search, or optimization) problem to be NP-hard if solving it in polynomial time would imply P = NP. Definition implicitly uses Turing reduction (extended to search problems).

Q. What's so hard about factoring an integer N in polynomial time - can't I just divide all potential factors less than N (or √N) into x and see if any have a remainder of zero?

A. The algorithm is correct, but remember it takes only lg N bits to represent the integer N. Thus, for an algorithm to be polynomial in the input size, it must be polynomial in lg N, and not N.

Q. How is it possible that checking whether an integer is composite is solvable in polynomial time, yet finding its factors is not known (or believed) to be?

A. There are ways to prove a number is composite without getting your hands on any of its factors. A famous theorem from number theory (Fermat's little theorem) implies that if you have two integers a and p such that (i) a is not a multiple of p and (ii) a^p-1 != 1 (mod p), then p is not prime.

Q. Is there a decision problem that is polynomial solvable on a quantum computers, but provably not in P?

A. This is an open research problem. FACTOR is a candidate, but there is no proof that FACTOR is not in P, although this is widely believed to be outside P.

Q. Does NP = EXPTIME?

A. The experts believe no, but have been unable to prove it.

Q. Suppose someone proves P = NP. What would be the practical consequences?

A. It depends on how the question is resolved. Obviously, it would be a remarkable theoretical breakthrough. In practice, it might have dramatic significance if the proof of P = NP established a fast algorithm for an important NP-complete problem. If the proof results in an 2^100 N^117 algorithm for the TSP (and the constant and exponent could not be reduced), it would not have little practical impact. It could also be that someone proves P = NP by indirect means, thereby yielding no algorithm at all!

Q. Suppose someone proves P != NP. What would be the practical consequences?

A. It would be a remarkable theoretical breakthrough and solidify the foundation of much of computational complexity.

Q. Suppose P = NP. Does that mean deterministic TM are the same as non-deterministic TM?

A. Not quite. For example, even if P = NP, a non-deterministic TM may be able to solve a problem in time proportional to N^2, where the best deterministic one would take N^3. If P = NP, it just means that the two types of machines solve the same set of decision problems in polynomial time, but it says nothing about the degree of the polynomial.

Q. Where can I learn more about NP-completeness?

A. The authoritative reference remains Garey and Johnson Computers and Intractability: A Guide to the Theory of NP-completeness. Many of the most important subsequent discoveries are documented in David Johnson's NP-completeness column.

Exercises

Suppose that X is NP-complete, X poly-time reduces to Y, and Y poly-time reduces to X. Is Y necessarily NP-complete?
Answer: No, since Y may not be in NP. For example if X = CIRCUIT-SAT and Y = CO-CIRCUIT-SAT then X and Y satisfy the conditions, but it is unknown whether Y is in NP. Note that the answer depends on our definition of poly-time reduction (to be Turing reductions and not Karp reductions).

Explain why the optimization version of the vertex cover problem is not necessarily a search problem.

Answer: There does not appear to be an efficient way to certify that a purported solution is the best possible (even though we could use binary search on the search version of the problem to find the best solution).

Web Exercises

Subset sum. Given N positive integers and a target value V, determine if there is a subset whose sum is exactly V. Divide the integers into 4 equal groups. Enumerate and store all of the subset sums in each group by brute force. Let A, B, C, and D denote the subset sums of the four groups. The goal is to find integers a, b, c, and d such that a + b + c + d = V, where a is in A, b is in B, c is in C, and d is in D. Now, use a heap to enumerate the sums a + b where a is in A and b is in B. Simultaneously, use another heap to enumerate the sums c + d in decreasing order, where c is in C and d is in D.
Sum of square roots. What is the minimum nonzero difference between two sums of square roots of integers? Given n and k, find the minimum positive value of
| √a₁ + √a₂ + ... + √a_k - √b₁ - √b₂ - ... - √b_k |
where ai and bi are between 0 and n. For example r(20, 2) = √10 + √11 - √5 - √18 and r(20, 3) = √5 + √6 + √18 - √4 - √12 - √12. Hint: enumerate all 2^(n/2) sums of square roots of the first n/2 integers and let that set be A, enumerate all 2^(n/2) sums of square roots of the last n/2 integers and let that be B. Now enumerate sums of a + b in sorted order, where a is in A and b is in B. Look for sums whose difference is very tiny.
Dividing diamonds. Given N (around 36) class D diamonds, divide them into two groups so that they are as close in total weight to each other as possible. Assume the weights are real numbers (measured in carats).
Hamilton path in DAG. Given a directed acyclic graph G, give an O(n+m)-time algorithm to test whether or not it is Hamiltonian. Hint: topological sort.
Which of the following can we infer from the fact that the traveling salesperson problem is NP-complete, if we assume that P is not equal to NP?
1. There does not exist an algorithm that solves arbitrary instances of the TSP problem.
2. There does not exist an algorithm that efficiently solves arbitrary instances of the TSP problem.
3. There exists an algorithm that efficiently solves arbitrary instances of the TSP problem, but no one has been able to find it.
4. The TSP is not in P.
5. All algorithms that are guaranteed to solve the TSP run in polynomial time for some family of input points.
6. All algorithms that are guaranteed to solve the TSP run in exponential time for all families of input points.
Answer: (b) and (d) only.
Which of the following can we infer from the fact that PRIMALITY is in NP but not known to be NP-complete, if we assume that P is not equal to NP?
1. There exists an algorithm that solves arbitrary instances of PRIMALITY.
2. There exists an algorithm that efficiently solves arbitrary instances of PRIMALITY.
3. If we found an efficient algorithm for PRIMALITY, we could immediately use it as a black box to solve TSP.
Answer: We can infer only (a) since all problems in P are decidable. If P != NP, then there are problems in NP that are neither in P or NP-complete. PRIMALITY could be one of them (although this was recently disproved). Part (c) cannot be inferred since we don't know if PRIMALITY is NP-complete.
Which of the following are NP-complete?
1. The brute force TSP algorithm.
2. The quicksort algorithm for sorting.
3. The Halting problem.
4. Hilbert's 10th problem.
Answer: None. NP-completeness deals with *problems* not specific algorithm for problems. The Halting problem and Hilbert's 10th problem are undecidable, so they are not in NP (and all NP-complete problems are in NP).
Let X and Y be two decision problems. Suppose we know that X reduces to Y. Which of the following can we infer?
1. If Y is NP-complete then so is X.
2. If X is NP-complete then so is Y.
3. If Y is NP-complete and X is in NP then X is NP-complete.
4. If X is NP-complete and Y is in NP then Y is NP-complete.
5. X and Y can't both be NP-complete.
6. If X is in P, then Y is in P.
7. If Y is in P, then X is in P.
Answer: (d) and (g) only. X reduces to Y means that if you had a black box to solve Y efficiently, you could use it to solve X efficiently. X is no harder than Y.
Show that CIRCUIT-SAT reduces to CIRCUIT-DIFF. Hint: create a circuit with N inputs that always outputs 0.
Show that CIRCUIT-DIFF reduces to CIRCUIT-SAT.
Show that DETERMINANT is in NP: given an N-by-N integer matrix A, is det(A) = 0?
Solution: certificate is a nonzero vector x such that Ax = 0.
Show that FULL-RANK is in NP: given an N-by-N integer matrix A, is det(A) ≠ 0?
Solution: certificate is an N-by-N inverse matrix B such that AB = I.
Search problems vs. decision problems. We can formulate a search problem using a corresponding decision problem. For example, the problem of finding the prime factorization of an integer N can be formulate using the decision problem: given two integers N and and L, does N have a nontrivial factor strictly less than L. The search problem is solvable in polynomial time if and only if the corresponding decision problem is. To see why, we can efficiently find the smallest factor p of N by using different values of L along with binary search. Once we have the factor p, we can repeat the process on N/p.
Usually we can show that the search problem and the decision problem are equivalent up to polynomial factors in running time. Papadimitriou (Example 10.8) gives an interesting counterexample to the rule. Given N positive integers such that their sum is less than 2^N - 1, find two subsets whose sum is equal. For example, the 10 numbers below sum to 1014 < 1023.
23 47 59 88 91 100 111 133 157 205

Since there are more subsets of N integers (2^N) than numbers between 1 and 1014, there must be two different subsets with the same sum. But nobody know a polynomial time algorithm for finding such a subset. On the other hand, the natural decision problem is trivial solvable in constant time: are there two subsets of numbers that sum to the same value?
Pratt's primality certificate. Show that PRIMES is in NP. Use Lehmer's theorem (Fermat's Little Theorem Converse) which asserts that an integer p > 1 is prime if and only if there exists an integer x such that x^N-1 = 1 (mod p) and x^(p-1)/d ≠ 1 (mod p) for all prime divisors d of p-1. For example, if N = 7919, then the prime factorization of p-1 = 7918 = 2 × 37 × 107. Now x = 7 satisfies 7⁷⁹¹⁸ = 1 (mod 7919), but 7^7918/2 ≠ 1 (mod 7919), 7^7918/37 ≠ 1 (mod 7919), 7^7918/107 ≠ 1 (mod 7919). This proves that 7919 is prime (assuming that you recursively certify that 2, 37, and 107 are prime).
Pell's equation. Find all positive integer solutions to Pell's equation: x^2 - 92y^2 = 1. Solution: (1151, 120), (2649601, 276240), etc. There are infinitely many solutions, but each successive one is about 2300 times the previous one.
Pell's equation. In 1657, Pierre Fermat challenged his colleagues with the following problem: given a positive integer c, find a positive integer y such that cy² is a perfect square. Fermat used c = 109. It turns out the smallest solution is (x, y) = (158,070,671,986,249, 15,140,424,455,100). Write a program Pell.java that reads in an integer c and finds the smallest solution to Pell's equation: x² - c y² = 1. Try c = 61. The smallest solution is (1,766,319,049, 226,153,980). For c = 313, the smallest solution is ( 3,218,812,082,913,484,91,819,380,158,564,160). The problem is provably unsolvable in a polynomial number of steps (as a function of the number of bits in the input c) because the output may require exponentially many bits!
3-COLOR reduced to 4-COLOR. Show that 3-COLOR polynomial reduces to 4-COLOR. Hint: given an instance G of 3-COLOR, create an instance G' of 4-COLOR by adding a special vertex x to G and connecting it to all of the vertices in G.
3-SAT is self-reducible. Show that 3-SAT is self-reducible. That is, given an oracle that answers whether or not any 3-SAT formula is satisfiable, design an algorithm that can find a satisfying assignment to a 3-SAT formula (assuming it is satisfiable). Your algorithm should run in polynomial time plus a polynomial number of calls to the oracle.
3-COLOR is self-reducible. Show that 3-COLOR is self-reducible. That is, given an oracle that answers whether or not any graph G is 3-colorable, design an algorithm that can 3-color a graph (assuming it is 3-colorable). Your algorithm should run in polynomial time plus a polynomial number of calls to the oracle.