3.3 Balanced Search Trees
This section under major construction.
We introduce in this section a type of binary search tree
where costs are guaranteed to be logarithmic.
Our trees have near-perfect balance, where the height is guaranteed to be no
larger than 2 lg N.
2-3 search trees.
The primary step to get the flexibility that we need to guarantee balance in search trees is to allow the nodes in our trees to hold more than one key.Definition.
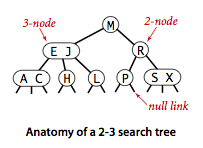
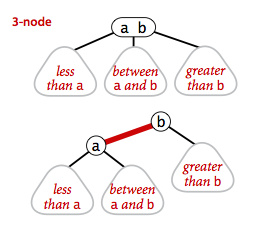
A 2-3 search tree is a tree that either is empty or:- A 2-node, with one key (and associated value) and two links, a left link to a 2-3 search tree with smaller keys, and a right link to a 2-3 search tree with larger keys
- A 3-node, with two keys (and associated values) and three links, a left link to a 2-3 search tree with smaller keys, a middle link to a 2-3 search tree with keys between the node's keys and a right link to a 2-3 search tree with larger keys.
- Search.
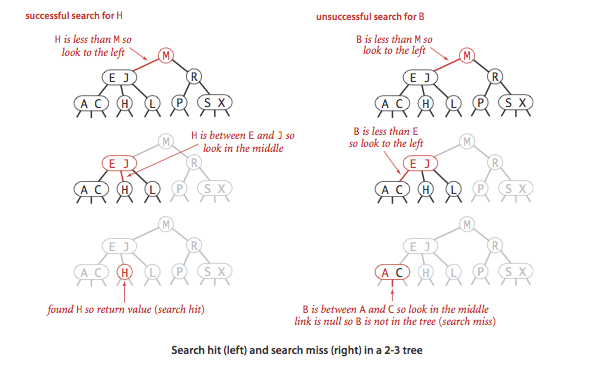
To determine whether a key is in a 2-3 tree, we compare it against
the keys at the root: If it is equal to any of them, we have a search hit;
otherwise, we follow the link from the root to the subtree corresponding
to the interval of key values that could contain
the search key, and then recursively search in that subtree.
- Insert into a 2-node.
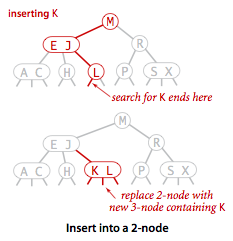
To insert a new node in a 2-3 tree, we might do an unsuccessful search and then hook on the
node at the bottom, as we did with BSTs, but the new tree would not remain perfectly balanced.
It is easy to maintain perfect balance if the node at which the search terminates
is a 2-node: We just replace the node with a 3-node containing its key and the new key to be
inserted.
- Insert into a tree consisting of a single 3-node.
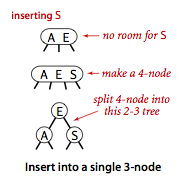
Suppose that we want to insert into a tiny 2-3 tree consisting of just a single 3-node.
Such a tree has two keys, but no room for a new key in its one node. To be able to perform the
insertion, we temporarily put the new key into a 4-node,
a natural extension of our node type that has three keys and four links.
Creating the 4-node is convenient because it is easy to
convert it into a 2-3 tree made up of three 2-nodes, one with the middle key (at the root),
one with the smallest of the three keys (pointed to by the left link of the root), and one
with the largest of the three keys (pointed to by the right link of the root).
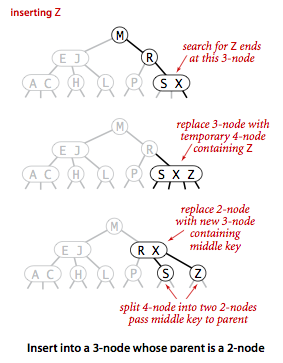
- Insert into a 3-node whose parent is a 2-node.
Suppose that the search ends at a 3-node at the bottom whose parent is a 2-node.
In this case, we can still make room for the new key while maintaining
perfect balance in the tree, by making a temporary 4-node
as just described, then splitting the 4-node as just described, but then,
instead of creating a new node to hold the middle key, moving the middle key
to the nodes parent.
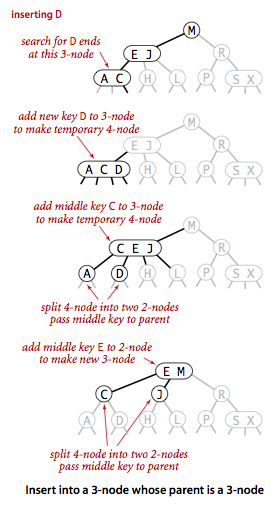
- Insert into a 3-node whose parent is a 3-node.
Now suppose that the search ends at a node whose parent is a 3-node. Again, we make a
temporary 4-node as just described, then split it and insert its middle key into the parent.
The parent was a 3-node, so we replace it with a temporary new 4-node containing the middle
key from the 4-node split. Then, we perform precisely the same transformation on that node.
That is we split the new 4-node and insert its middle key into its parent.
Extending to the general case is clear: we continue up the tree,
splitting 4-nodes and inserting their middle keys in their parents until
reaching a 2-node, which we replace with a 3-node that does not to
be further split, or until reaching a 3-node at the root.
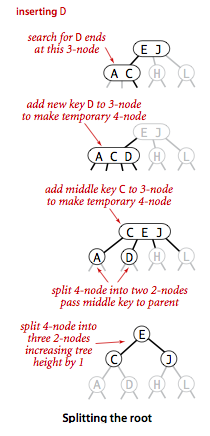
- Splitting the root.
If we have 3-nodes along the whole path from the insertion point to the
root, we end up with a temporary 4-node at the root. In this case we
split the temporary 4-node into three 2-nodes.
- Local transformations. The basis of the 2-3 tree insertion algorithm is that all of these transformations are purely local: No part of the 2-3 tree needs to be examined or modified other than the specified nodes and links. The number of links changed for each transformation is bounded by a small constant. Each of the transformations passes up one of the keys from a 4-node to that nodes parent in the tree, and then restructures links accordingly, without touching any other part of the tree.
- Global properties. These local transformations preserve the global properties that the tree is ordered and balanced: the number of links on the path from the root to any null link is the same.
Proposition.
Search and insert operations in a 2-3 tree with N keys are guaranteed to visit at most lg N nodes.
However, we are only part of the way to an implementation. Although it would be possible to write code that performs transformations on distinct data types representing 2- and 3-nodes, most of the tasks that we have described are inconvenient to implement in this direct representation.
Red-black BSTs.
The insertion algorithm for 2-3 trees just described is not difficult to understand. We consider a simple representation known as a red-black BST that leads to a natural implementation.- Encoding 3-nodes.
The basic idea behind red-black BSTs is to encode 2-3 trees by starting with standard BSTs
(which are made up of 2-nodes) and adding extra information to encode 3-nodes. We think of the
links as being of two different types: red
links, which bind together two 2-nodes to represent
3-nodes, and black links, which bind together the 2-3 tree.
Specifically, we represent 3-nodes
as two 2-nodes connected by a single red link that leans left.
We refer to BSTs that represent 2-3 trees in this way as
red-black BSTs.
One advantage of using such a representation is that it allows us to use our get() code for standard BST search without modification.
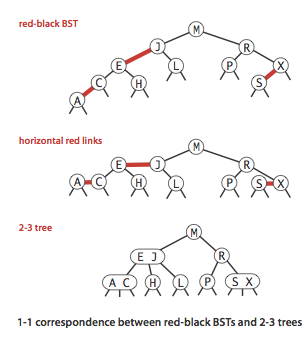
- A 1-1 correspondence.
Given any 2-3 tree, we can immediately derive a corresponding red-black BST, just by
converting each node as specified.
Conversely, if we draw the red links horizontally in a red-black BST,
all of the null links are the same
distance from the root, and if we then collapse together the nodes connected
by red links, the result is a 2-3 tree.
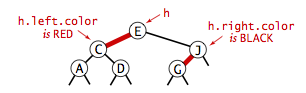
- Color representation.
Since each node is pointed to by precisely one link (from its
parent), we encode the color of links in nodes,
by adding a boolean instance variable color to our
Node data type, which is true if the link from
the parent is red and false if it is black.
By convention, null links are black.
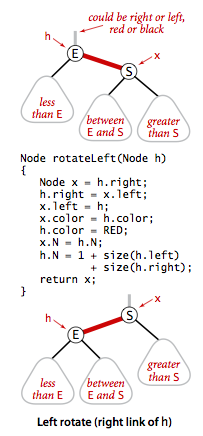
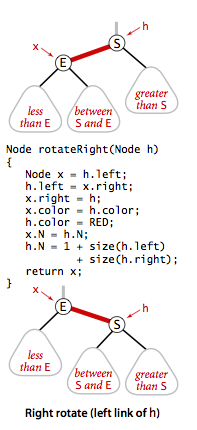
- Rotations. The implementation that we will consider might allow right-leaning red links or two red-links in a row during an operation, but it always corrects these conditions before completion, through judicious use of an operation called rotation that switches orientation of red links. First, suppose that we have a right-leaning red link that needs to be rotated to lean to the left. This operation is called a left rotation. Implementing a right rotation that converts a left-leaning red link to a right-leaning one amounts to the same code, with left and right interchanged.
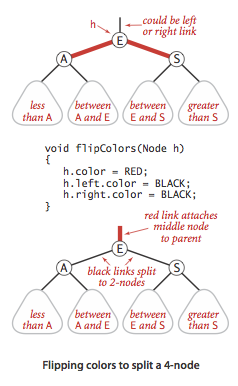
- Flipping colors.
The implementation that we will consider might also allow a black parent to have
two red children.
The color flip operation flips the colors of the
the two red children to black and the color of the black parent to red.
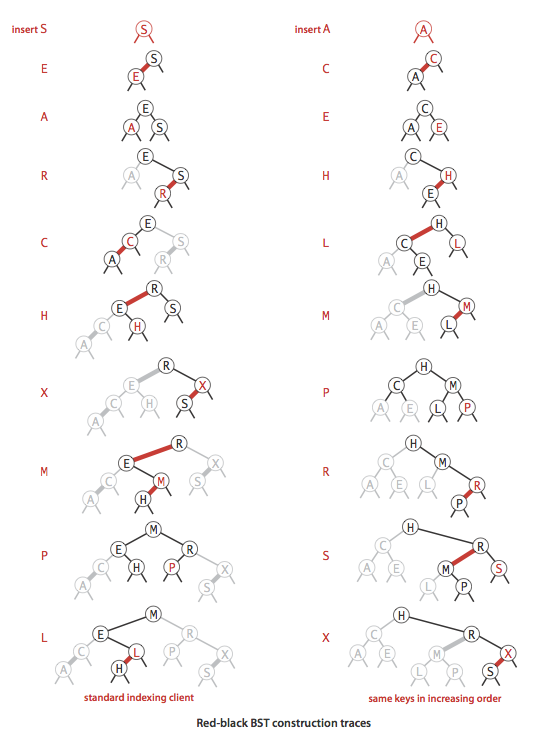
- Insert into a single 2-node.
- Insert into a 2-node at the bottom.
- Insert into a tree with two keys (in a 3-node).
- Keeping the root black.
- Insert into a 3-node at the bottom.
- Passing a red link up the tree.
Implementation.
Program RedBlackBST.java implements a left-leaning red-black BST. Program RedBlackLiteBST.java is a simpler version that only implement put, get, and contains.
Deletion.
Proposition.
The height of a red-blackBST with N nodes is no more than 2 lg N.Proposition.
In a red-black BST, the following operations take logarithmic time in the worst case: search, insertion, finding the minimum, finding the maximum, floor, ceiling, rank, select, delete the minimum, delete the maximum, delete, and range count.Property.
The average length of a path from the root to a node in a red-black BST with N nodes is ~1.00 lg N.Visualization.
The following visualization shows 255 keys inserted into a red-black BST in random order.
Exercises
-
Which of the follow are legal balanced red-black BSTs?
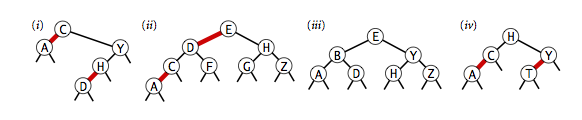
Solution. (iii) and (iv) only. (i) is not balanced, (ii) is not in symmetric order or balanced.
- True or false: If you insert keys in increasing order into a red-black BST, the tree height is monotonically increasing.
-
Draw the red-black BST that results when you insert letters
A through K in order into an initially empty
red-black BST. Then, describe what happens in general when
red-black BSTs are built by inserting keys in ascending order.
Solution. The following visualization shows 255 keys inserted into a red-black BST in ascending order.
-
Answer the previous two questions for the case when
the keys are inserted in descending order.
Solution. False. The following visualization shows 255 keys inserted into a red-black BST in descending order.
- Create a test client TestRedBlackBST.java.
Creative Problems
- Certification. Add to RedBlackBST.java a method is23() to check that no node is connected to two red links and that there are no right-leaning red links. Add a method isBalanced() to check that all paths from the root to a null link have the same number of black links. Combine these methods with isBST() to create a method isRedBlackBST() that checks that the tree is a BST and that it satisfies these two conditions.
-
Fundamental theorem of rotations.
Show that any BST can be transformed into any other BST on the same
set of keys by a sequence of left and right rotations.
Solution sketch: rotate the smallest key in the first BST to the root along the leftward spine; then recur with the resulting right subtree until you have a tree of height N (with every left link null). Do the same with the second BST. Remark: it is unknown whether there exists a polynomial-time algorithm for determining the minimum number of rotations needed to transform one BST into the other (even though the rotation distance is at most 2N - 6 for BSTs with at least 11 nodes).
- Delete the minimum. Implement the deleteMin() operation for RedBlackBST.java by maintaining the correspondence with the transformations given in the text for moving down the left spine of the tree while maintaining the invariant that the current node is not a 2-node.
- Delete the maximum. Implement the deleteMax() operation for RedBlackBST.java. Note that the transformations involved differ slightly from those in the previous exercise because red links are left-leaning.
- Delete. Implement the delete() operation for RedBlackBST.java, combining the methods of the previous two exercises with the delete() operation for BSTs.
Web Exercises
- Given a sorted sequence of keys, describe how to construct a red-black BST that contains them in linear time.
-
Suppose that you do a search in a red-black BST that
terminates unsuccessfully after following 20 links from the root.
Fill in the blanks below with the best (integer) bounds that you
can infer from this fact about any unsuccessful search
- Must follow at least ______ links from the root
- Need follow at most _______ links from the root
- With 1 bit per node we can represent 2-, 3-, and 4-nodes. How many bits would we need to represent 5-, 6-, 7-, and 8-nodes.
- Substring reversing.
Given a string of length N, support the following operations:
select(i) = get the ith character, and reverse(i, j) = reverse the
substring from i to j.
Solution sketch. Maintain the string in a balanced search tree, where each node records the subtree count and a reverse bit (that interchanges the role of the left and right children if there are an odd number of reverse bits on the path from the root to the node). To implement select(i), do a binary search starting at the root, using the subtree counts and reverse bits. To implement reverse(i, j), split the BST at select(i) and select(j) to form three BSTs, reverse the bit of the middle BST, and join them back together using a join operation. Maintain the subtree counts and reverse bits when rotating.
- Memory of a BST.
What is the memory usage of a BST and RedBlackBST and TreeMap?
Solution. MemoryOfBSTs.java.
- Randomized BST.
Program RandomizedBST.java implements
a randomized BST, including deletion.
Expected O(log N) performance per operations.
Expectation depends only on the randomness in the algorithm; it does
not depend on the input distribution.
Must store subtree count field in each node; generates
O(log N) random numbers per insert.
Proposition. Tree has same distribution as if the keys were inserted in random order.
- Join. Write a function that takes two randomized BSTs as input and returns a third randomized BST which contains the union of the elements in the two BSTs. Assume no duplicates.
- Splay BST. Program SplayBST.java implements a splay tree.
- Randomized queue. Implement a RandomizedQueue.java so that all operations take logarithmic time in the worst case.
- Red-black BST with many updates. When performing a put() with a key that is already in a red-black BST, our RedBlackBST.java performs many unnecessary calls to isRed() and size(). Optimize the code so that these calls are skipped in such situations.


