6.1 Geometric Primitives

This chapter under construction.

Points in the plane.

Program Point.java is a data type for points in the plane. It contains methods for drawing and computing the distance to another point. We make the instance variables x and y to be public and final so that the client can read the coordinates of point p with p.x and p.y. (This is consistent with the way Java implements Point and Point2D.Double, although our data type is immutable!)

Counterclockwise turns. Given three points a, b, and c, determine whether they form a counterclockwise angle. The function ccw takes three Point inputs a, b, and c and returns +1 if a->b->c is a counterclockwise angle, -1 if a->b->c is a clockwise angle, and 0 if a->b->c are collinear. Use the following determinant formula which gives twice the (signed) area of the triangle a->b->c. If the area is positive, then a->b->c is counterclockwise; if the area is negative, then a->b->c is clockwise; if the area is zero then a->b->c are collinear.

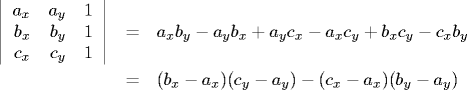
The second version might be more efficient since fewer multiplications and additions. Susceptible to overflow error - consider using long integers for intermediate results.

public static int ccw(Point a, Point b, Point c) {
   return (b.x - a.x) * (c.y - a.y) - (c.x - a.x) * (b.y - a.y);
}

Line segment intersection. Represent a line segment by its two endpoints. Write a method intersects so that s1.intersects(s2) returns true if the two line segments properly intersect and false otherwise. Simple idea: form equations of two line segments and check for potential intersection by solving system of two equations in two unknowns. Better approach if only need to know whether the segments intersect (and not the intersection point itself) - avoids issues of floating-point precision.

We assume no three or more points are collinear. We describe how to remove this assumption later. First, we consider intersections where two segments intersect at a point interior to both segments. For simplicitly, The line segments (ap, aq) and (bp, bq) properly intersect if (i) ap and aq are on different sides of the line defined by (bp, bq) and (ii) bp and bq are on different sides of the line defined by (ap, aq). To determine (i) we perform two ccw tests; to determine (ii) we perform two additional ccw tests.

public boolean intersects(Segment b) {
   Segment a = this;
   if (Point.ccw(a.p, a.q, b.p) * Point.ccw(a.p, a.q, b.q) > 0) return false;
   if (Point.ccw(b.p, b.q, a.p) * Point.ccw(b.p, b.q, a.q) > 0) return false;
   return true;
}

Degeneracies. The test above ignores situations where three or more endpoints are collinear. This includes the case if one or both of the line segments degenerate to a single point. See figure XYZ for some possible cases. Usesful subroutine is: given 3 collinear points a, b, and c, is b between a and c? Need to handle vertical line-segment case separately. Also need to worry about segments that degenerate to a single point. Surprisingly difficult to get it right.

Two line segments (ap, aq) and (bp, bq) intersect (properly or inproperly) if either

(ap, aq, bp) and (ap, aq, bq) have different orientations and (bp, bq, ap) and (bp, bq, aq) have different orientations.
(ap, aq, bp), (ap, aq, bq), (bp, bq, ap), and (bp, bq, aq) are all collinear and the x-projections of the two line segments intersect and the y-projections of the two line segments intersect.

This condition works even if the segments are degenerate.

Finding the point of intersection. Determining the point at which two line segments intersect takes us into the realm of floating-point computation or rational arithmetic. To determine if the two line segments a-b and c-d intersect, compute

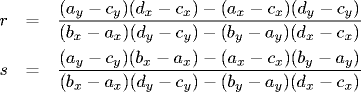
If 0 ≤ r ≤ 1 and 0 ≤ s ≤ 1, then the line segments intersect. Moreover, the point of intersection is (x, y) = (a_x + r(b_x-a_x), a_y + r(b_y-a_y)). If the denominator in equation 1 is zero, a-b and c-d are parallel. If the numerator in equation 1 is also zero, then a-b and c-d are collinear.

Computational geometry.

We create a number of data types for geometric objects in the plane. Although we will only introduce a tiny set of computational geometry primitives, they arise in numerous applications, including computer graphics (movies, games, virtual reality), computer vision, data mining, VLSI design, mathematical models of the physical world (maps, architecture, medical imaging), astronomical simulations, scientific computing, and and geographic information systems.

Intervals. An interval is defined by two Comparable objects of the same type. Program Interval.java represents a 1D interval.
Intervals. A 2D interval is defined by two 1D intervals, possibly of different types. (Maybe we should make them the same type for simplicity since that's all we need.) Program Interval2D.java represents a 2D interval.
Polygons. Polygons are a useful mathematical abstraction for representing the shapes of real-world objects (letters for optical character recognition, obstacles to be avoided by a robot, US congressional district, pieces of an airfoil). Program Polygon.java is a data type for closed polygons. A polygon is a sequence of points p₀ through p_N, where we assume the first point is equal to the last point, i.e., the polygon is closed. The perimeter is the sum of the Euclidean distances of the N line segments. The signed area of a non self-intersecting polygon is given by

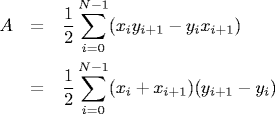
The polygon is counterclockwise if the area is positive. We assume the points are indexed 0 through N-1 and that point N equals point 0. The centroid (or center of mass) of a non self-intersecting polygon is given by the point (x, y) where x and y are defined by

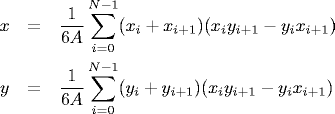
To draw a shaded polygon on screen, we need to know whether each pixel (i, j) is inside or outside the polygon. Jordan curve theorem implies any polygon partitions plane into a finite inside region and an infinite outside region. Solution (ray crossing method): draw a ray from (i, j) down and count the number of times it crosses the polygon (even = outside, odd = inside). Intution: think of polygon as a fence and count # times you jump over the fence.

Reference: David Eppstein. winding number calculation

Exercises

Re-implement BoundingBox.java using two Point objects as instance variables instead of 4 doubles.
Add a method orientation to Polygon.java that returns +1 if the orientation is counter-clockwise and -1 if it is clockwise. Hint: the orientation is the sign of the signed area.
Bounding boxes. Create a data type BoundingBox.java that represents a bounding box. A bounding box is an axis-aligned rectangle. We implement by specifying its lower left endpoint (x1, y1) and its upper right endpoint (x2, y2). [Could implement with a 2D interval of integers.] The method contains returns true if the invoking bounding box contains a given point. The method intersects determines whether two bounding boxes intersect. Also area and perimeter methods. Add a constructor to BoundingBox.java that take an array of points, and initializes the smallest bounding box containing each point. Add a method union so that a.union(b) creates and returns a new BoundingBox that is the smallest bounding box that contains both a and b.
Given a set of N points, determine if all N are collinear in O(N) time. Use only integer arithmetic.
Given a set of N intervals, find the largest interval (not necessarily one of the N) that intersects as many of the N intervals as possible. Hint: simulate a sweep line running from -infinity to + infinity, adding the interval to a data structure when its left endpoint is encountered, and deleting the interval when its right endpoint is encountered.
Modify Interval2D.java to create a data type for 3D intervals of a single parameterized type.
Modify Interval2D.java so that its two intervals can be of different parameterized types, e.g., integers on the x-axis and strings on the y-axis.
Create a data type Line.java that represents a line in the plane. Implement a line by including two Point data members or one Point and a slope.
Create a data type Circle.java for circles in the plane. We represent a circle by its center (a Point) and its radius (a double). It contains methods for computing the area and perimeter, determining whether a Point is inside the circle, and determining whether two circles intersect.
Devise a formula for the area of a quadrilateral. Ideally, it should be just as efficient as the one for the area of a triangle (5 additions, 2 multiplications) Reference

Consider the following implementation of ccw.

public static int ccw(Point a, Point b, Point c) {
   int dx1 = b.x - a.x;
   int dx2 = b.y - a.y;
   int dx3 = c.x - a.x;
   int dx4 = c.x - a.x;
   if      (dx1*dy2 < dy1*dx2)                     return +1;
   else if (dx1*dy2 < dy1*dx2)                     return -1;
   else if (dx1*dx2 < 0 || dy1*dy2 < 0)            return -1;
   else if (dx1*dx1 + dy1*dy1 < dx2*dx2 + dy2*dy2) return +1;
   else                                            return  0;
}

Give a (degenerate) input where the following line segment intersection test fails.

public boolean intersectsP(Segment b) {
   Segment a = this;
   return (Point.ccw(a.p, a.q, b.p) * Point.ccw(a.p, a.q, b.q) <= 0) &&
          (Point.ccw(b.p, b.q, a.p) * Point.ccw(b.p, b.q, a.q) <= 0);
}

Answer: If the line segment a is a single point and it lies in the interior of the line segment b. If the line segments are non-degenerate, the above is an efficient test for line segment intersection.

Write a program that generates N circles at random in the unit box of diameter 0.05, draws them to the screen, and highlights all those pairs that overlap.
Bullseye. Create several concentric circles and associate a value with each circle. Generate a point at random (using some distribution). The number of points you score is the value of the smallest enclosing circle.
Random sphere packing. Generate random disks of diameter d in the unit square and repeatedly add each new one as long as it doesn't intersect an existing disk. Stop trying when 100 attempts in-a-row fail. How many disks on average are placed? Use the Circle.java data type.
Create a data type Line.java that represents a line in the plane. Implement a line by including two Point data members or one Point and a slope.
Write a method distanceTo that computes the shortest distance from a point (x, y) to the line specified by (x₁, y₁) and (x₂, y₂). The formula is

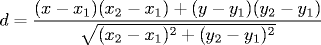
Note that the denominator is the distance between the two points on the line so you should reuse the distanceTo method in Point. The numerator is signed, so this returns the signed distance - you may wish to take absolute values.
Create a data type Triangle that represents a triangle. It should have a constructor which take references to three Point objects as inputs and create a triangle with those endpoints. It should have methods area, perimeter, isIsosceles, isRight, isEquilateral, and isScalene.
Write a client program Pi.java that estimates the mathematical constant π using Monte Carlo simulation. Create a circle centered at (1/2, 1/2) of radius 1/2. Then repeatedly generate random points in the unit square and check if they are inside the circle. Print out the fraction of points that fall inside the circle. The true answer estimates π / 4 since the ratio of the area of the circle to the area of the square is π / 4.
Simple polygon. Given N points in the plane, design an algorithm to find a simple polygon connecting the points. O(N log N): sort by polar angle with respect to rightmost lowest point. Theta(N log N): applies even if points are on a circle - to sort N real numbers, map angles to points on the circle.
Point in a convex polygon. Write a program that can test whether points fall within a convex polygon, using linear preprocessing time and logarithmic test time per point. First, read in the points which define the polygon. Assume that these appear in the standard format, the points appearing clockwise around the polygon with the point with lowest y coordinate first. Note that this implies that the y coordinates of the points increase, then decrease. During input, remember which point is at the "top" (where the y coordinates start to go down). This divides the polygon into a "right" part (increasing y coordinates) and a "left" part (decreasing y coordinates). In summary, after input, you have the points of the polygon in an array, and you have an index into the array which tells where the right part ends and the left part begins.
Next, read in some test points, testing, one at a time, whether or not each is inside the polygon, using the following method. If a horizontal line were drawn through the given test point, it would hit one line from the left part of the polygon and one line from the right part of the polygon. The point is inside the polygon if and only if it falls between those two lines. But from the way that the polygon is stored (the y coordinates of each part are sorted), the two lines can be found in logarithmic time using binary search. After the two lines are found, it is a simple matter to test whether the point falls between them.
Largest empty rectangle. Given a set of n points in the plane, with coordinates between 0 and 1,000, find the area of the largest rectangle that contains no points.
Largest area under a histogram. Given a histogram of n points 1..n. The height of point i is h_i. Find the largest axis-aligned rectangle that fits under the histogram. O(n log n) is good. O(n) is also possible.
Helipad landing. Given an n-by-n grid of integer altitudes values, find the largest axis-aligned rectangle that contains values of all the same height. Reference: ???
Intersection between line and line segment. Line intersects line segment iff one of the endpoints of the line segment is to the left and one is to the right. (Ignores degeneracies.)
Volume of tetrahedron. Formula for volume of a triangle extends to volume of a d-dimensional simplex in natural way. The following determinant is 1/6 times the volume of a tetrahedron.
| ax ay az 1 | 1 | bx by bz 1 | - | cx cy cz 1 | 6 | dx dy dz 1 |
In general, the d-by-d determinant is 1/d! times time volume of the corresponding d-dimensional simplex.

In-circle test. Determine if the point d lies inside or outside the circle defined by the three points a, b, and c in the plane. Application: primitive operation in Delaunay triangulation algorithms. Assuming that a, b, c are labeled in counter-clockwise order around the circle, compute the determinant:

| ax  ay  ax^2 + ay^2  1 |
| bx  by  bx^2 + by^2  1 |
| cx  cy  cx^2 + cy^2  1 |
| dx  dy  dx^2 + dy^2  1 |

adx = ax - dx;
ady = ay - dy;
bdx = bx - dx;
bdy = by - dy;
cdx = cx - dx;
cdy = cy - dy;

abdet = adx * bdy - bdx * ady;
bcdet = bdx * cdy - cdx * bdy;
cadet = cdx * ady - adx * cdy;
alift = adx * adx + ady * ady;
blift = bdx * bdx + bdy * bdy;
clift = cdx * cdx + cdy * cdy;

return alift * bcdet + blift * cadet + clift * abdet;

The determinant is positive if d is inside the circle, negative if d is outside the circle, and zero if all four points are cocircular. This generalizes to higher dimensions, e.g., point inside a sphere defined by 4 points.

Pattern recognition. Given a list of N points in the plane, find all subset of 3 or more points that are collinear.
Pattern recognition. Given a list of N points in the plane in general position (no three are collinear), find a new point p that is not collinear with any pair of the N original points.