4.3 Minimum Spanning Trees
Minimum spanning tree.
An edge-weighted graph is a graph where we associate weights or costs with each edge. A minimum spanning tree (MST) of an edge-weighted graph is a spanning tree whose weight (the sum of the weights of its edges) is no larger than the weight of any other spanning tree.
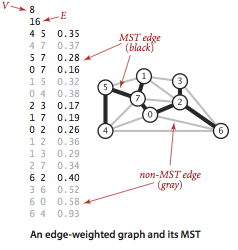
Assumptions.
To streamline the presentation, we adopt the following conventions:- The graph is connected. The spanning-tree condition in our definition implies that the graph must be connected for an MST to exist. If a graph is not connected, we can adapt our algorithms to compute the MSTs of each of its connected components, collectively known as a minimum spanning forest.
- The edge weights are not necessarily distances. Geometric intuition is sometimes beneficial, but the edge weights can be arbitrary.
- The edge weights may be zero or negative. If the edge weights are all positive, it suffices to define the MST as the subgraph with minimal total weight that connects all the vertices.
- The edge weights are all different. If edges can have equal weights, the minimum spanning tree may not be unique. Making this assumption simplifies some of our proofs, but all of our our algorithms work properly even in the presence of equal weights.
Underlying principles.
We recall two of the defining properties of a tree:- Adding an edge that connects two vertices in a tree creates a unique cycle.
- Removing an edge from a tree breaks it into two separate subtrees.
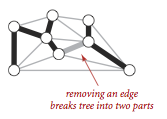
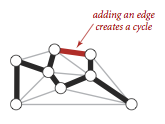
A cut of a graph is a partition of its vertices into two
disjoint sets. A crossing edge is an edge that connects a vertex
in one set with a vertex in the other.
We recall For simplicity, we assume all edge weights are distinct.
Under this assumption, the MST is unique.
Define cut and cycle.
The following properties lead to a number of MST algorithms.
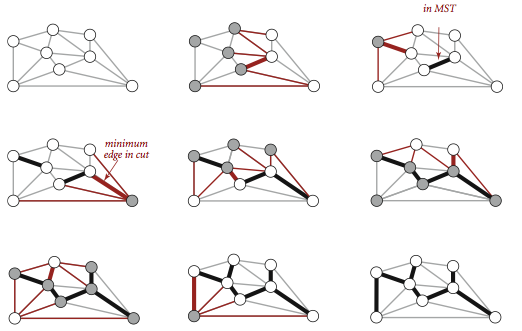
Proposition. (Cut property)
Given any cut in an edge-weighted graph (with all edge weights distinct), the crossing edge of minimum weight is in the MST of the graph.
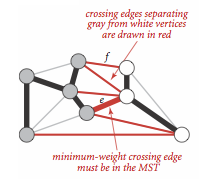
The cut property is the basis for the algorithms that we consider for
the MST problem. Specifically, they are special cases of the
greedy algorithm.
Proposition. (Greedy MST algorithm)
The following method colors black all edges in the the MST of any connected edge-weighted graph with V vertices: Starting with all edges colored gray, find a cut with no black edges, color its minimum-weight edge black, and continue until V-1 edges have been colored black.
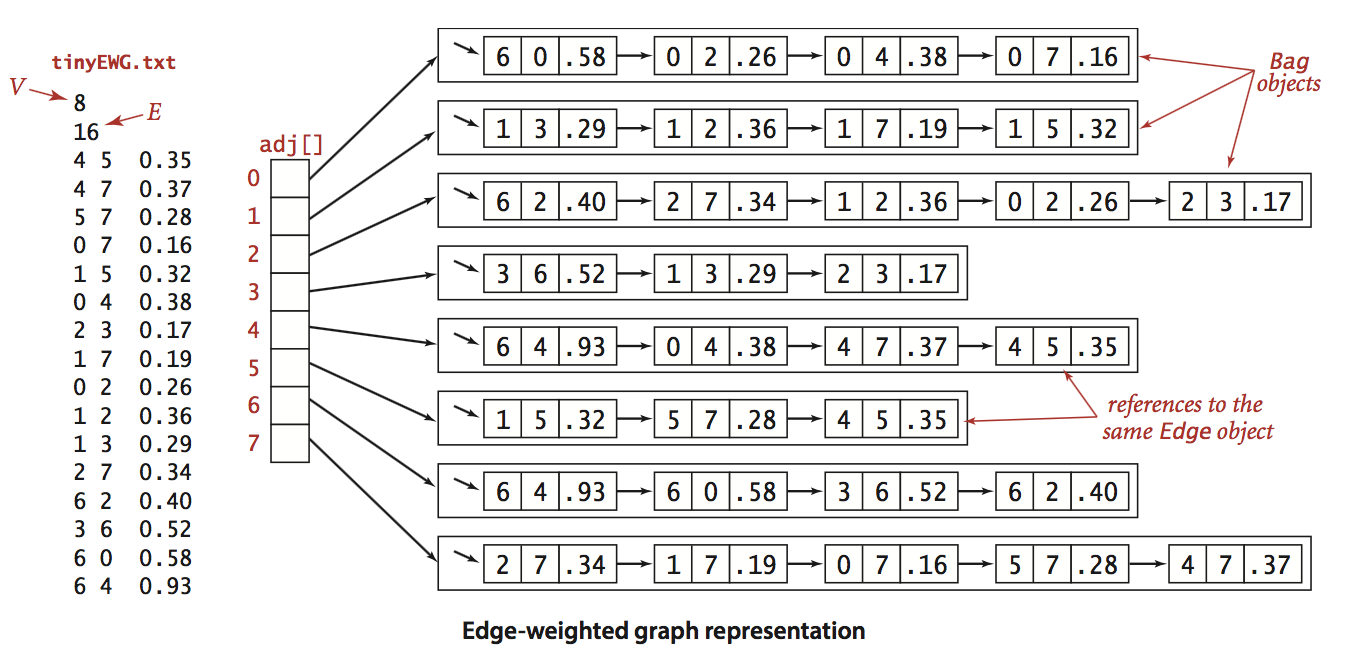
Edge-weighted graph data type.
We represent the weighted edges using the following API:

The either() and other() methods are useful
for accessing the edge's vertices; the compareTo() method
compares edges by weight.
Edge.java is a straightforward
implementation.
We represent edge-weighted graphs using the following API:

We allow parallel edges and self-loops.
EdgeWeightedGraph.java
implements the API using the adjacency-lists representation.
MST API.
We use the following API for computing an MST of an edge-weighted graph:

We prepare some test data:
- tinyEWG.txt contains 8 vertices and 16 edges
- mediumEWG.txt contains 250 vertices and 1,273 edges
- 1000EWG.txt contains 1,000 vertices and 8,433 edges
- 10000EWG.txt contains 10,000 vertices and 61,731 edges
- largeEWG.txt contains one million vertices and 7,586,063 edges
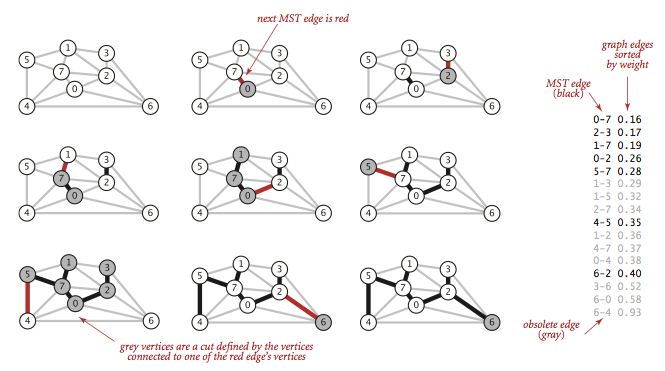
Prim's algorithm.
Prim's algorithm works by attaching a new edge to a single growing tree at each step: Start with any vertex as a single-vertex tree; then add V-1 edges to it, always taking next (coloring black) the minimum-weight edge that connects a vertex on the tree to a vertex not yet on the tree (a crossing edge for the cut defined by tree vertices).
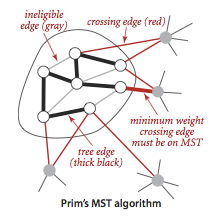
The one-sentence description of Prim's algorithm leaves unanswered a
key question: How do we (efficiently) find the crossing edge of
minimal weight?
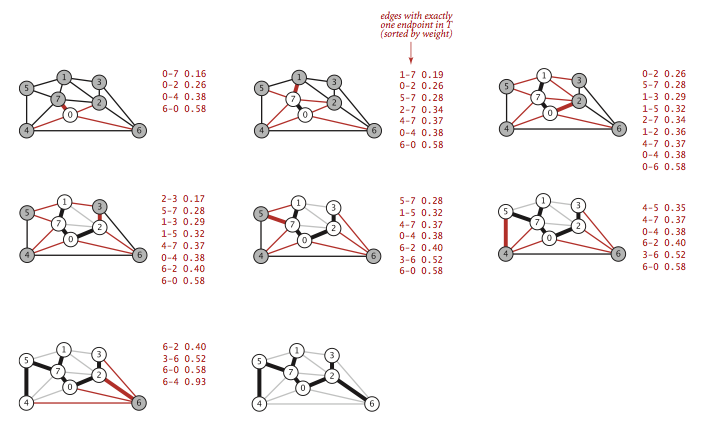
- Lazy implementation.
We use a priority queue to hold the
crossing edges and find one of minimal weight.
Each time that we add an edge to the tree, we also add a vertex to the
tree. To maintain the set of crossing edges,
we need to add to the priority queue all edges from that vertex to
any non-tree vertex.
But we must do more: any edge connecting the
vertex just added to a tree vertex that is already on the priority queue now
becomes ineligible (it is no longer a crossing edge because
it connects two tree vertices).
The lazy implementation leaves such edges on the priority
queue, deferring the ineligibility test to when we remove them.
LazyPrimMST.java is an implementation of this lazy approach. It relies on the MinPQ.java priority queue.
- Eager implementation.
To improve the lazy implementation of Prim's algorithm, we might try
to delete ineligible edges from the priority queue, so that the
priority queue contains only the crossing edges.
But we can eliminate even more edges. The key is to note that our
only interest is in the minimal edge
from each non-tree vertex to a tree vertex. When we add a vertex v to
the tree, the only
possible change with respect to each non-tree vertex w is that adding
v brings w closer
than before to the tree. In short, we do not need to keep on the
priority queue all of the
edges from w to vertices tree—we just need to keep track of the
minimum-weight edge
and check whether the addition of v to the tree necessitates that we
update that minimum (because of an edge v-w that has lower weight),
which we can do as we process
each edge in s adjacency list. In other words, we maintain on the
priority queue just
one edge for each non-tree vertex: the shortest edge that connects it
to the tree.
PrimMST.java is an implementation of this eager approach. It relies on the IndexMinPQ.java indexed priority queue to perform the decrease-key operation.
Proposition.
Prim's algorithm computes the MST of any connected edge-weighted graph. The lazy version of Prim's algorithm uses space proportional to E and time proportional to E log E (in the worst case) to compute the MST of a connected edge-weighted graph with E edges and V vertices; the eager version uses space proportional to V and time proportional to E log V (in the worst case).
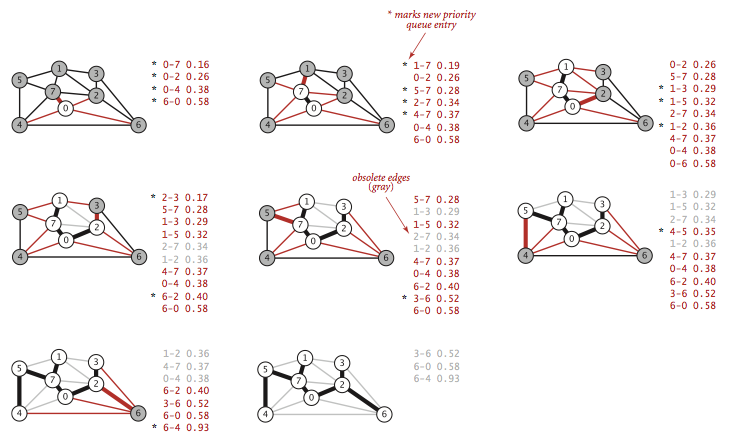
Kruskal's algorithm.
Kruskal's algorithm processes the edges in order of their weight values (smallest to largest), taking for the MST (coloring black) each edge that does not form a cycle with edges previously added, stopping after adding V-1 edges. The black edges form a forest of trees that evolves gradually into a single tree, the MST.
To implement Kruskal's algorithm, we use a priority queue to consider the edges
in order by weight, a union-find data structure to identify those that cause
cycles, and a queue to collect the MST edges.
Program KruskalMST.java
implements Kruskal's algorithm along these lines. It uses the helper
MinPQ.java,
UF.java, and
Queue.java data types.
Proposition.
Kruskal's algorithm computes the MST of any connected edge-weighted graph with E edges and V vertices using extra space proportional to E and time proportional to E log E (in the worst case).
Exercises
-
Prove that you can rescale the weights by adding a positive
constant to all of them or by multiplying them all by a positive constant
without affecting the MST.
Solution. Kruskal's algorithm accesses the edge weights only through the compareTo() method. Adding a positive constant to each weight (or multiplying by a positive constant) won't change the result of the compareTo() method.
-
Show that if a graph's edges all have distinct weights, the MST is unique.
Solution. For the sake of contradiction, suppose there are two different MSTs of G, say T1 and T2. Let e = v-w be the min weight edge of G that is in one of T1 or T2, but not both. Let's suppose e is in T1. Adding e to T2 creates a cycle C. There is at least one edge, say f, in C that is not in T1 (otherwise T1 would be cyclic). By our choice of e, w(e) ≤ w(f). Since all of the edge weights are distinct, w(e) < w(f). Now, replacing f with e in T2 yields a new spanning tree with weight less than that of T2 (contradicting the minimality of T2).
-
How would you find a maximum spanning tree of an edge-weighted graph?
Solution. Negative the weight of each edge (or reverse the sense of comparison in the compareTo() method).
- Implement the constructor for EdgeWeightedGraph.java that reads an edge-weighted graph from an input stream.
-
Determine the amount of memory used by
EdgeWeightedGraph.java
to represent a graph with V vertices and E edges, using the memory-cost model
of Section 1.4.
Solution. 56 + 40V + 112E. MemoryOfEdgeWeightedGraph.java computes it empirically assuming that no Integer values are cached—Java typically caches the integers -128 to 127.
-
Given an MST for an edge-weighted graph G, suppose that an edge in G
that does not disconnect G is deleted.
Describe how to find an MST of the new graph in time proportional to E.
Solution. If the edge in not in the MST, then the old MST is an MST of the updated graph. Otherwise, deleting the edge from the MST leaves two connected components. Add the minimum weight edge with one vertex in each component.
-
Given an MST for an edge-weighted graph G
and a new edge e, describe how to find an MST of the new graph in time proportional to V.
Solution. Add edge e to the MST creates a unique cycle. Delete the maximum weight edge on this cycle.
- Implement toString() for EdgeWeightedGraph.java.
-
Suppose that you implement an eager version of Prim's algorithm but instead
of using a priority queue to find the next vertex to add to the tree,
you scan through all V entries in the distTo[] array to find
the non-tree vertex with the smallest value.
What would be the order of growth of the worst-case running time for the
eager version of Prim's algorithm on graphs with V vertices and E edges?
When would this method be appropriate, if ever? Defend your answer.
Solution. Prim's algorithm would run in time proportional to V^2, which is optimal for dense graphs.
- Provide an implementation of edges() for PrimMST.java.
Creative Problems
- Minimum spanning forest.
Develop versions of Prim's and Kruskal's algorithms that compute
the minimum spanning forest of an edge-weighted graph that
is not necessarily connected.
Solution. PrimMST.java and KruskalMST.java accomplish this.
- Certification.
Write a method check() that
uses the following cut optimality conditions
to verify that a proposed set of edges is in fact an MST:
A set of edges is an MST if it is a spanning tree and every
edge is a minimum-weight edge in the cut defined by removing
that edge from the tree.
What is the order of growth of the running time of your method?
Solution. KruskalMST.java.
Experiments
- Boruvka's algorithm.
Develop an implementation BoruvkaMST.java
of Boruvka's algorithm:
Build an MST by adding edges to a growing forest of trees,
as in Kruskal's algorithm, but in stages.
At each stage, find the minimum-weight edge that connects each tree
to a different one, then add all such edges to the MST.
Assume that the edge weights are all different, to avoid cycles.
Hint: Maintain in a vertex-indexed array to identify
the edge that connects each component to its nearest neighbor,
and use the union-find data structure.
Remark. There are a most log V phases since number of trees decreases by at least a factor of 2 in each phase. Attractive because it is efficient and can be run in parallel.
Web Exercises
- Minimum bottleneck spanning tree.
A minimum bottleneck spanning tree of an edge-weighted graph G
is a spanning tree of G such that minimizes the maximum weight
of any edge in the spanning tree.
Design an algorithm to find a minimum bottleneck spanning tree.
Solution. Every MST is a minimum bottleneck spanning tree (but not necessarily the converse). This can be proved using the cut property.
- Minimum median spanning tree.
A minimum median spanning tree of an edge-weighted graph G
is a spanning tree of G such that minimizes the median of its weights.
Design an efficient algorithm to find a minimum median spanning tree.
Solution. Every MST is a minimum median spanning tree (but not necessarily the converse).
- Maze generation. Create a maze using a randomized version of Kruskal or Prim's algorithm.
- Unique MST. Design an algorithm to determine if the MST is unique for a given graph G.
- Random spanning tree. Given a graph G, generate a spanning tree of G, uniformly at random. Using the following remarkable theorem of Aldous and Broder: Start at an arbitrary vertex s and take a random walk until every vertex has been visited (choosing an outgoing edge uniformly at random among all incident edges). If a vertex has never been visited before, add the edge to that vertex to the spanning tree T. Then T is a uniformly random spanning tree of G. The expected running time is bounded by the cover time of G, which is at most proportional to EV.
- Minimum-weight feedback edge set. A feedback edge set of a graph is a subset of edges that contains at least one edge from every cycle in the graph. If the edges of a feedback edge set are removed, the resulting graph will be acyclic. Design an efficient algorithm to find a feedback edge set of minimum weight in an edge-weighted graph with positive edge weights.
- Distribution of edge weights in two MSTs. Suppose than an edge-weighted digraph has two MSTs T1 and T2. Prove that if T1 has k edges of weight w, then T2 has k edges of weight w.
- USA Computing Olympiad problem.
In a city there are N houses, each of which is in need of a water supply.
It costs w[i] dollars to build a
well at house i, and it costs c[i][j] to build a pipe in between houses i and j.
A house can receive water if either there is a well built there or there is some
path of pipes to a house with a well.
Design an algorithm to find the minimum amount of money needed to supply every house with water.
-->
Solution.: Create an edge-weighted graph with N+1 vertices (one for each house plus a source vertex x). Include an edge between every pair of vertices i and j with cost c[i][j] (to represent the potential pipes). Include an edge between the source s and every house i with cost w[i] (to represent the potential open wells). Find an MST in this edge-weighted graph.
- Spanning tree with exactly k orange edges. Given a graph with edges colored either orange or black, design a linearithmic algorithm to find a spanning tree that contains exactly k orange edges (or report that no such spanning tree exists).
- Minimum variance spanning tree. Given a connected edge weighted graph, find a minimum spanning tree that minimizes the variance of its edge weights.


