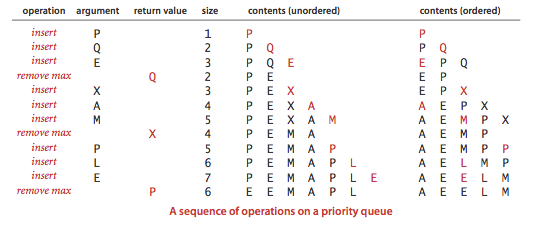
2.4 Priority Queues
Many applications require that we process items having keys in order,
but not necessarily in full sorted order and not necessarily all at once.
Often, we collect a set of items, then process the one
with the largest key, then perhaps collect more items, then process
the one with the current largest key, and so forth.
An appropriate data type in such an environment supports two operations:
remove the maximum and insert.
Such a data type is called a priority queue.
API.
Priority queues are characterized by the remove the maximum and insert operations. By convention, we will compare keys only with a less() method, as we have been doing for sorting. Thus, if records can have duplicate keys, maximum means any record with the largest key value. To complete the API, we also need to add constructors and a test if empty operation. For flexibility, we use a generic implementation with a generic type Key that implements Comparable.

Program TopM.java is a priority queue client that takes a command-line argument M, reads transactions from standard input, and prints out the M largest transactions.
Elementary implementations.
The basic data structures that we discussed in Section 1.3 provide us with four immediate starting points for implementing priority queues.- Array representation (unordered). Perhaps the simplest priority queue implementation is based on our code for pushdown stacks. The code for insert in the priority queue is the same as for push in the stack. To implement remove the maximum, we can add code like the inner loop of selection sort to exchange the maximum item with the item at the end and then delete that one, as we did with pop() for stacks. Program UnorderedArrayMaxPQ.java implements a priority queue using this approach.
- Array representation (ordered). Another approach is to add code for insert to move larger entries one position to the right, thus keeping the entries in the array in order (as in insertion sort). Thus the largest item is always at the end, and the code for remove the maximum in the priority queue is the same as for pop in the stack. Program OrderedArrayMaxPQ.java implements a priority queue using this approach.
- Linked-list representations (unordered and reverse-ordered). Similarly, we can start with our linked-list code for pushdown stacks, either modifying the code for pop() to find and return the maximum or the code for push() to keep items in reverse order and the code for pop() to unlink and return the first (maximum) item on the list.
All of the elementary implementations just discussed have the property that either the insert or the remove the maximum operation takes linear time in the worst case. Finding an implementation where both operations are guaranteed to be fast is a more interesting task, and it is the main subject of this section.
Heap definitions.
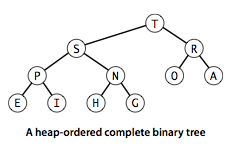
The binary heap is a data structure that can efficiently support the basic priority-queue operations. In a binary heap, the items are stored in an array such that each key is guaranteed to be larger than (or equal to) the keys at two other specific positions. In turn, each of those keys must be larger than two more keys, and so forth. This ordering is easy to see if we view the keys as being in a binary tree structure with edges from each key to the two keys known to be smaller.Definition. A binary tree is heap-ordered if the key in each node is larger than (or equal to) the keys in that nodes two children (if any).
Proposition. The largest key in a heap-ordered binary tree is found at the root.
We can impose the heap-ordering restriction on any binary tree. It is particularly convenient, however, to use a complete binary tree like the one below.
Definition. A binary heap is a set of nodes with keys arranged in a complete heap-ordered binary tree, represented in level order in an array (not using the first entry).
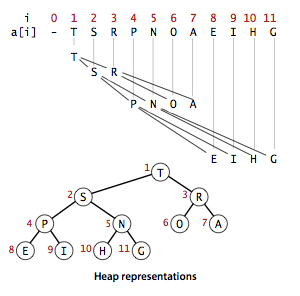
In a heap, the parent of the node in position k is in position k/2; and, conversely, the two children of the node in position k are in positions 2k and 2k + 1. We can travel up and down by doing simple arithmetic on array indices: to move up the tree from a[k] we set k to k/2; to move down the tree we set k to 2*k or 2*k+1.
Algorithms on heaps.
We represent a heap of size n in private array pq[] of length n + 1, with pq[0] unused and the heap in pq[1] through pq[n]. We access keys only through private helper functions less() and exch(). The heap operations that we consider work by first making a simple modification that could violate the heap condition, then traveling through the heap, modifying the heap as required to ensure that the heap condition is satisfied everywhere. We refer to this process as reheapifying, or restoring heap order.- Bottom-up reheapify (swim).
If the heap order is violated because a node's key becomes larger than
that node's parents key, then we can make progress toward fixing the
violation by exchanging the node with its parent. After the exchange, the node is larger
than both its children (one is the old parent, and the other is smaller than
the old parent because it was a child of that node)
but the node may still be larger than its parent.
We can fix that violation in the same way, and so forth, moving up the heap until we
reach a node with a larger key, or the root.
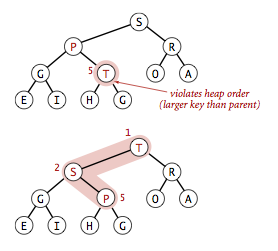
private void swim(int k) { while (k > 1 && less(k/2, k)) { exch(k, k/2); k = k/2; } }
- Top-down heapify (sink).
If the heap order is violated because a node's key becomes
smaller than one or both of that node's children's keys, then we can make progress
toward fixing the violation by exchanging the node with the larger of its two children.
This switch may cause a violation at the child; we fix that violation in the same way,
and so forth, moving down the heap until we reach
a node with both children smaller, or the bottom.
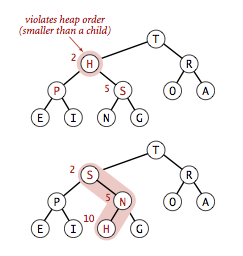
private void sink(int k) { while (2*k <= N) { int j = 2*k; if (j < N && less(j, j+1)) j++; if (!less(k, j)) break; exch(k, j); k = j; } }
Heap-based priority queue.
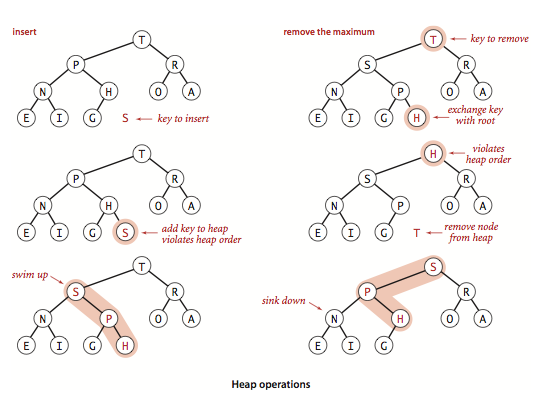
These sink() and swim() operations provide the basis for efficient implementation of the priority-queue API, as diagrammed below and implemented in MaxPQ.java and MinPQ.java.- Insert. We add the new item at the end of the array, increment the size of the heap, and then swim up through the heap with that item to restore the heap condition.
- Remove the maximum. We take the largest item off the top, put the item from the end of the heap at the top, decrement the size of the heap, and then sink down through the heap with that item to restore the heap condition.
Proposition.
In an n-item priority queue,
the heap algorithms require no more than 1 + lg n compares
for insert and no more than 2 lg n compares for
remove the maximum.
Practical considerations.
We conclude our study of the heap priority queue API with a few practical considerations.- Multiway heaps. It is not difficult to modify our code to build heaps based on an array representation of complete heap-ordered ternary or d-ary trees. There is a tradeoff between the lower cost from the reduced tree height and the higher cost of finding the largest of the three or d children at each node.
- Array resizing. We can add a no-argument constructor, code for array doubling in insert(), and code for array halving in delMax(), just as we did for stacks in Section 1.3. The logarithmic time bounds are amortized when the size of the priority queue is arbitrary and the arrays are resized.
- Immutability of keys. The priority queue contains objects that are created by clients but assumes that the client code does not change the keys (which might invalidate the heap invariants).
- Index priority queue.
In many applications, it makes sense to allow clients to refer to
items that are already on the priority queue.
One easy way to do so is to associate a unique integer index with each item.

IndexMinPQ.java is a heap-based implementation of this API; IndexMaxPQ.java is similar but for maximum-oriented priority queues. Multiway.java is a client that merges together several sorted input streams into one sorted output stream.
Heapsort.
We can use any priority queue to develop a sorting method. We insert all the keys to be sorted into a minimum-oriented priority queue, then repeatedly use remove the minimum to remove them all in order. When using a heap for the priority queue, we obtain heapsort.Focusing on the task of sorting, we abandon the notion of hiding the heap representation of the priority queue and use swim() and sink() directly. Doing so allows us to sort an array without needing any extra space, by maintaining the heap within the array to be sorted. Heapsort breaks into two phases: heap construction, where we reorganize the original array into a heap, and the sortdown, where we pull the items out of the heap in decreasing order to build the sorted result.
- Heap construction. We can accomplish this task in time proportional to n lg n,by proceeding from left to right through the array, using swim() to ensure that the entries to the left of the scanning pointer make up a heap-ordered complete tree, like successive priority queue insertions. A clever method that is much more efficient is to proceed from right to left, using sink() to make subheaps as we go. Every position in the array is the root of a small subheap; sink() works or such subheaps, as well. If the two children of a node are heaps, then calling sink() on that node makes the subtree rooted there a heap.
- Sortdown. Most of the work during heapsort is done during the second phase, where we remove the largest remaining items from the heap and put it into the array position vacated as the heap shrinks.
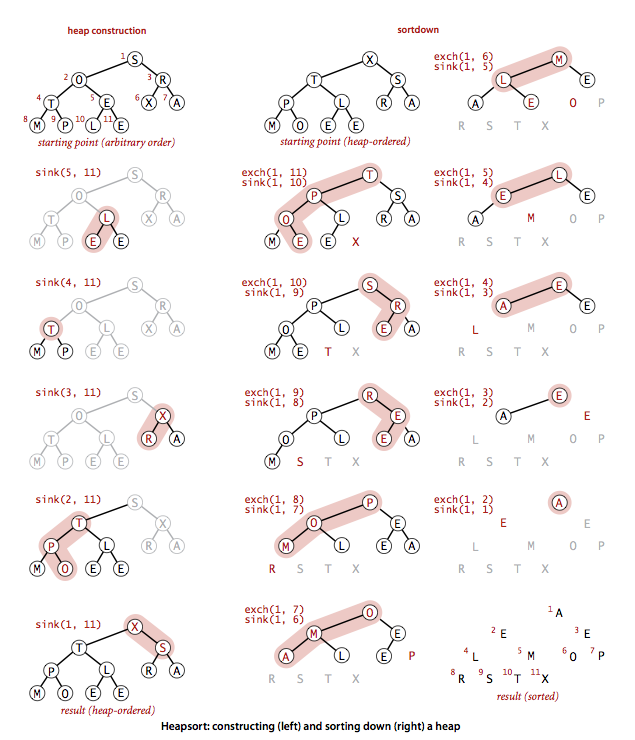
Heap.java is a full implementation of heapsort.
Below is a trace of the contents of the array after each sink.
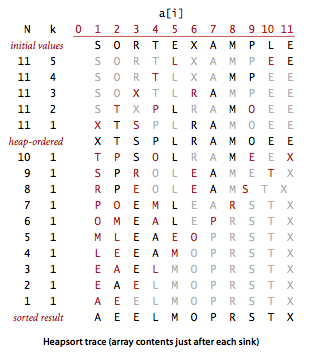
Proposition.
Sink-based heap construction is linear time.
Proposition.
Heapsort users fewer than 2 n lg n compare and exchanges to sort n items.
Most items reinserted into the heap during sortdown go all the way to the bottom. We can thus save time by avoiding the check for whether the item has reached its position, simply promoting the larger of the two children until the bottom is reached, then moving back up the heap to the proper position. This idea cuts the number of compares by a factor of 2 at the expense of extra bookkeeping.
Exercises
- Suppose that the sequence
(where a letter means insert and an asterisk means remove the maximum) is applied to an initially empty priority queue. Give the sequence of values returned by remove the maximum operations.P R I O * R * * I * T * Y * * * Q U E * * * U * E
- Criticize the following idea: to implement find the maximum
in constant time, why not keep track of the maximum value inserted so far,
then return that value for find the maximum?
Solution. Will need to update the maximum value from scratch after a remove-the-maximum operation.
- Provide priority queue implementations that support
insert and remove the maximum, one for each of the following
underlying data structures: unordered array, ordered array, unordered linked
list, and ordered linked list.
Give a table of the worst-case bounds for each operation for
each of your four implementations from the previous exercise.
Partial solution. OrderedArrayMaxPQ.java and UnorderedArrayMaxPQ.java
- Is an array that is sorted in decreasing order a max-oriented heap.
- Suppose that your application will have a huge number of insert operations, but only a few remove the maximum operations. Which priority-queue implementation do you think would be most effective: heap, unordered array, ordered array?
- Suppose that your application will have a huge number of find the maximum operations, but a relatively small number of insert and remove the maximum operations. Which priority queue implementation do you think would be most effective: heap, unordered array, ordered array?
- What is the minimum number of items that must be exchanged during a remove the maximum operation in a heap of size n with no duplicate keys? Give a heap of size 15 for which the minimum is achieved. Answer the same question for two and three successive remove the maximum operations.
-
Design a linear-time certification algorithm to check whether an array
pq[] is a min-oriented heap.
Solution. See the isMinHeap() method in MinPQ.java.
-
Prove that sink-based heap construction uses at most 2n compares
and at most n exchanges.
Solution. It suffices to prove that sink-based heap construction uses fewer than n exchanges because the number of compares is at most twice the number of exchanges. For simplicity, assume that the binary heap is perfect (i.e., a binary tree in which every level is completely filled) and has height h.
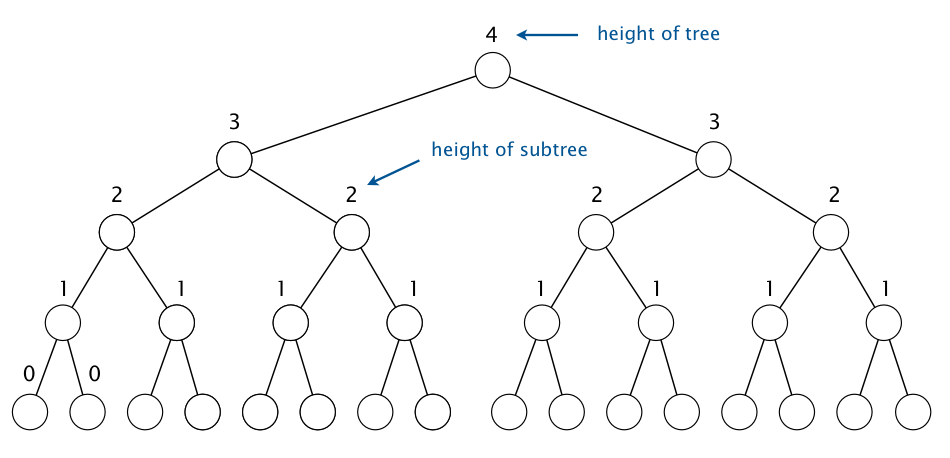
We define the height of a node in a tree to be the height of the subtree rooted at that node. A key at height k can be exchanged with at most k keys beneath it when it is sunk down. Since there are 2h−k nodes at height k, the total number of exchanges is at most: $$ \begin{eqnarray*} h + 2(h-1) + 4(h-2) + 8(h-3) + \ldots + 2^h (0) & = & 2^{h+1} - h - 2 \\ & = & n - (h+1) \\ & \le & n \end{eqnarray*} $$
The first equality is for a nonstandard sum, but it is straightforward to verify that the formula holds via mathematical induction. The second equality holds because a perfect binary tree of height h has 2h+1 − 1 nodes.
Proving that the result holds when the binary tree is not perfect requires a bit more care. You can do so using the fact that the number of nodes at height k in a binary heap on n nodes is at most ceil(n / 2k+1).
Alternate solution. We define the height of a node in a tree to be the height of the subtree rooted at that node.
- First, observe that a binary heap on n nodes has n − 1 links (because each link is the parent of one node and every node has a parent link except the root).
- Sinking a node of height k requires at most k exchanges.
- We will charge k links to each node at height k, but not necessarily
the links on the path taken when sinking the node. Instead, we charge the node the
k links along the path from the node that goes left–right–right–right–....
For example, in the diagram below, the root
node is charged the 4 red links; the blue node is charged the 3 blue links; and so forth.
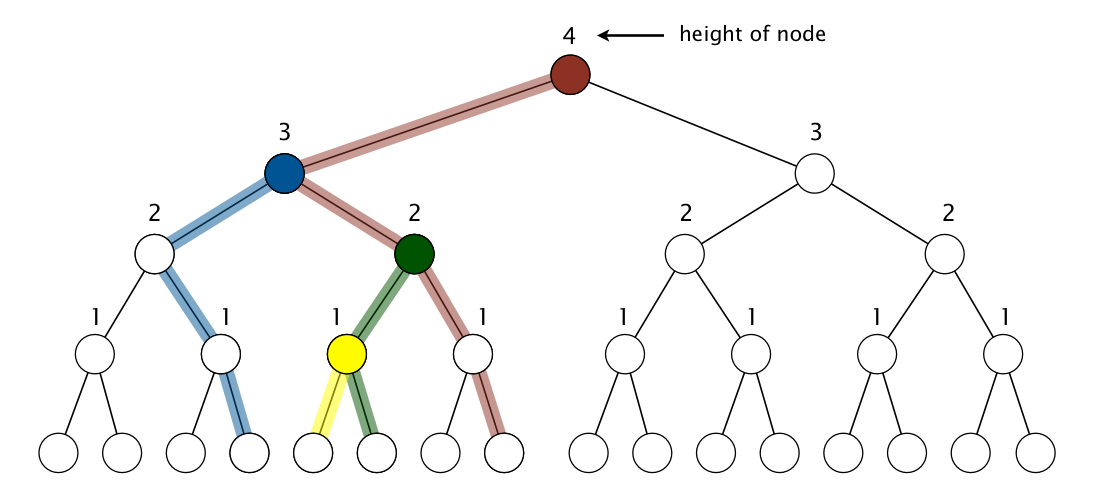
- Note that no link is charged to more than one node. (Links obtained by following only right links from the root are not charged to any node.)
- Thus, the total number of exchanges is at most n. Since there are at most 2 compares per exchange, the number of compares is at most 2n.
Creative Problems
- Computational number theory. Write a program CubeSum.java that prints out all integers of the form \(a^3 + b^3\) where \(a\) and \(b\) are integers between 0 and \(n<\) in sorted order, without using excessive space. That is, instead of computing an array of the \(n^2\) sums and sorting them, build a minimum-oriented priority queue, initially containing \((0^3, 0, 0), (1^3 + 1^3, 1, 1), (2^3 + 2^3, 2, 2), \ldots, (n^3 + n^3, n, n)\). Then, while the priority queue is nonempty, remove the smallest item \(i^3 + j^3,\; i, \; j)\), print it, and then, if \(j < n\), insert the item \((i^3 + (j+1)^3,\; i,\; j+1)\). Use this program to find all distinct integers \(a, b, c\), and \(d\) between 0 and \(10^6\) such that \(a^3 + b^3 = c^3 + d^3\), such as \(1729 = 9^3 + 10^3 = 1^3 + 12^3\).
- Find the minimum.
Add a min() method to
MaxPQ.java. Your implementation
should use constant time and constant extra space.
Solution: add an extra instance variable that points to the minimum item. Update it after each call to insert(). Reset it to null if the priority queue becomes empty.
- Dynamic-median finding.
Design a data type that supports insert in logarithmic
time, find the median in constant time, and
remove the median in logarithmic time.
Solution. Keep the median key in v; use a max-oriented heap for keys less than the key of v; use a min-oriented heap for keys greater than the key of v. To insert, add the new key into the appropriate heap, replace v with the key extracted from that heap.
- Lower bound.
Prove that it is impossible to develop an implementation of the MinPQ API such
that both insert and delete the minimum guarantee to use ~ n log log n compares.
Solution. This would yield an n log log n compare-based sorting algorithm (insert the n items, then repeatedly remove the minimum), violating the proposition of Section 2.3.
- Index priority-queue implementation. Implement IndexMaxPQ.java by modifying MaxPQ.java as follows: Change pq[] to hold indices, add an array keys[] to hold the key values, and add an array qp[] that is the inverse of pq[] — qp[i] gives the position of i in pq[] (the index j such that pq[j] is i). Then modify the code to maintain these data structures. Use the convention that qp[i] is -1 if i is not on the queue, and include a method contains() that tests this condition. You need to modify the helper methods exch() and less() but not sink() or swim().
Web Exercises
- Best, average, and worst case of heapsort.
What's are the best case, average case, and worst case number of compares
for heapsorting an array of length n?
Solution. If we allow duplicates, the best case is linear time (n equal keys); if we disallow duplicates, the best case is ~ n lg n compares (but the best case input is nontrivial). The average and worst case number of compares is ~ 2 n lg n compares. See The Analysis of Heapsort for details.
- Best and worst case of heapify.
What is the fewest and most number of compares/exchanges needed to heapify
an array of n items?
Solution. Heapifying an array of n items in descending order requires 0 exchanges and n − 1 compares. Heapifying an array of n items in ascending order requires ~ n exchanges and ~ 2n compares.
- Taxicab numbers. Find the smallest integers that can be expressed as the sum of cubes of integers in two different ways (1,729), three different ways (87,539,319), four different ways (6,963,472,309,248), five different ways (48,988,659,276,962,496), and six different ways (24,153,319,581,254,312,065,344). Such integers are named Taxicab numbers after the famous Ramanujan story. The smallest integers that can be expressed as the sum of cubes of integers in seven different ways is currently unknown. Write a program Taxicab.java that reads in a command line parameter N and prints out all nontrivial solutions of a3 + b3 = c3 + d3. such that a, b, c, and d, are less than or equal to N.
- Computational number theory. Find all solutions to the equation a + 2b2 = 3c3 + 4d4 for which a, b, c, and d are less than 100,000. Hint: use one min heap and one max heap.
- Interrupt handling. When programming a real-time system that can be interrupted (e.g., by a mouse click or wireless connection), it is necessary to attend to the interrupts immediately, before proceeding with the current activity. If the interrupts should be handled in the same order they arrive, then a FIFO queue is the appropriate data structure. However, if different interrupts have different priorities (e.g., ), then we need a priority queue.
- Simulation of queueing networks. M/M/1 queue for double parallel queues, etc. Difficult to analyze complex queueing networks mathematically. Instead use simulation to plot distribution of waiting times, etc. Need priority queue to determine which event to process next.
- Zipf distribution. Use the result of the previous exercise(s) to sample from the Zipfian distribution with parameter s and n. The distribution can take on integer values from 1 to n, and takes on value k with probability 1/k^s / sum_(i = 1 to n) 1/i^s. Example: words in Shakespeare's play Hamlet with s approximately equal to 1.
- Random process. Begin with n bins, each consisting one ball. Randomly select one of the n balls and move the ball to a bin at random such that the probability that a ball is placed in a bin with m balls is m/n. What is the distribution of balls that results after many iterations? Use the random sampling method described above to make the simulation efficient.
- Nearest neighbors. Given n vectors x1, x2, ..., xN of length m and another vector x of the same length, find the 20 vectors that are closest to x.
- Circle drawn on a piece of graph paper. Write a program to find the radius of a circle, centered on the origin, that touches 32 points with integer x- and y- coordinates. Hint: look for a number than can be expressed as the sum of two squares in several different ways. Answer: there are two Pythagorean triples with hypotenuse 25: 15^2 + 20^2 = 25^2, 7^2 + 24^2 = 25^2 yielding 20 such lattice points; there are 22 different Pythagorean triples with hypotenuse 5,525; this leads to 180 lattice points. 27,625 is smallest radius that touches more than 64. 154,136,450 has 35 Pythagorean triples.
- Perfect powers. Write a program PerfectPower.java to print out all perfect powers that can be represented as 64-bit long integers: 4, 8, 9, 16, 25, 27, .... A perfect power is a number that can be written as ab for integers a and b ≥ 2.
- Floating point additions. Add up n floating-point numbers, avoiding roundoff error. Delete smallest two: add two each other, and reinsert.
- First-fit for bin packing. 17/10 OPT + 2, 11/9 OPT + 4 (decreasing). Use max tournament tree in which players are N bins and value = available capacity.
- Stack with min/max.
Design a data type that supports push, pop, size, min, and max (where min and
max are the minimum and maximum items on the stack). All operations should
take constant time in the worst case.
Hint: Associate with each stack entry the minimum and maximum items currently on the stack.
- Queue with min/max.
Design a data type that supports enqueue, dequeue, size, min, and max (where min and
max are the minimum and maximum items on the queue). All operations should
take constant amortized time.
Hint: do the previous exercise and simulate a queue with two stacks.
- 2^i + 5^j. Print numbers of the form 2^i * 5^j in increasing order.
- Min-max heap.
Design a data structure that supports min and max in constant time,
insert, delete min, and delete max in logarithmic time by putting the items
in a single array of size n with the following properties:
- The array represents a complete binary tree.
- The key in a node at an even level is less than (or equal to) the keys in its subtree; the key in a node at an odd level is greater than (or equal to) the keys in its subtree.
- Range minimum query. Given a sequence of n items, a range minimum query from index i to j is the index of the minimum item between i and j. Design a data structure that preprocesses the sequence of n items in linear time to support range minimum queries in logarithmic time.
- Prove that a complete binary tree with n nodes has exactly ceiling(n/2) leaf nodes (nodes with no children).
- Max-oriented priority queue with min.
What is the order of growth of the running time to find a minimum key
in a maximum-oriented binary heap.
Solution: linear—the minimum key could be in any of the ceiling(n/2) leaf nodes.
- Max-oriented priority queue with min.
Design a data type that supports insert and remove-the-maximum
in logarithmic time along with both max an min in constant time.
Solution. Create a max-oriented binary heap and also store the minimum key inserted so far (which will never increase unless this heap becomes empty).
- kth largest item greater than x.
Given a maximum oriented binary heap, design an algorithm to determine whether
the kth largest item is greater than or equal to x. Your algorithm should run in time
proportional to k.
Solution: if the key in the node is greater than or equal to x, recursively search both the left subtree and the right subtree. Stop when the number of node explored is equal to k (the answer is yes) or there are no more nodes to explore (no).
- kth smallest item in a min-oriented binary heap.
Design a k log k algorithm to find the kth smallest item in a min-oriented
binary heap H containing n items.
Solution. Build a new min-oriented heap H'. We will not modify H. Insert the root of H into H' along with its heap index 1. Now, repeatedly delete the minimum item x in H' and insert into H' the two children of x from H. The kth item deleted from H' is the kth smallest item in H.
- Randomized queue. Implement a RandomQueue so that each operation is guaranteed to take at most logarithmic time. Hint: can't afford array doubling. No easy way with linked lists to locate a random element in O(1) time. Instead, use a complete binary tree with explicit links.
- FIFO queue with random deletion.
Implement a data type that supports the following operations:
insert an item, delete the item that was least recently added,
and delete a random item.
Each operation should take (at most) logarithmic time in the worst case.
Solution: Use a complete binary tree with explicit links; assign the long integer priority i to the ith item added to the data structure.
- Top k sums of two sorted arrays.
Given two sorted arrays a[] and b[], each of length n,
find the largest k sums of the form a[i] + b[j].
Hint: Using a priority queue (similar to the taxicab problem), you can achieve an O(k log n) algorithm. Surprisingly, it is possible to do it in O(k) time but the algorithm is complicated.
- Empirical analysis of heap construction. Empirically compare the linear-time bottom-up heap construction versus the naive linearithmic-time top-down heap construction. Be sure to comprae it over a range of values of n. LaMarca and Ladner report that because of cache locality, the naive algorithm can perform better in practice than the more clever approach for large values of n (when the heap no longer fits in the cache) even though the latter performs many fewer compares and exchanges.
- Empirical analysis of multiway heaps. Empirically compare the performance of 2- 4- and 8-way heaps. LaMarca and Ladner suggest several optimizations, taking into account caching effects.
- Empirical analysis of heapsort. Empirically compare the performance of 2- 4- and 8-way heapsort. LaMarca and Ladner suggest several optimizations, taking into account caching effects. Their data indicates that an optimized (and memory-tuned) 8-way heapsort can be twice as fast as classic heapsort.
- Heapify by insertions.
Suppose that you bulid a binary heap on n keys by repeatedly inserting the next key
into the binary heap. Show that the total number of compares is at most ~ n lg n.
Answer: the number of compares is at most lg 1 + lg 2 + ... + lg n = lg (n!) ~ n lg n.
- Heapify lower bound. (Gonnet and Munro)
Show that any compare-based algorithm for building a binary heap on n keys takes at least
~1.3644 N in the worst case.
Answer: use an information theoretic argument, ala sorting lower bound. There are n! possible heaps (permutation of the N integers) on n distinct keys, but there are many heaps that correspond to the same ordering. For example, there are two heaps (c a b and c b a) that correspond to the 3 elements a < b < c. For a perfect heap (with n = 2^h - 1), there are A(h) = n! / prod((2^k-1)^(2^(h-k)), k=1..h) heaps corresponding to the n elements a[0] < a[1] < ... < a[n-1]. (See Sloane sequence A056971.) Thus, any algorithm must be able to output one of P(h) = prod((2^k-1)^(2^(h-k)), k=1..h) possible answers. Using some fancy mathematics, you can argue that lg P(h) ~ 1.3644 n.
Note: The lower bound can be improved to ~ 3/2 n (Carlsson–Chen) using an adversary argument; the best-known algorithm for the problem takes ~ 1.625 n compares in the worst case (Gonnet and Munro).
- Stock exchange matching engine. Continuous limit order book: traders continuously post bids to buy or sell stock. A limit order means that a buyer (seller) places an order to buy (sell) a specified amount of a given stock at or below) (at or above) a given price. The order book displays buy and sell orders, and ranks them by price and then by time. Matching engine matches compatible buyers and sellers; if there are multiple possible buyers, break ties by choosing the buyer that placed the bid earliest. Use two priority queues for each stock, one for buyers and one for sellers.
- Random binary heap.
Suppose that you fill an array of length n with a random permutation of the integers 1 to n.
What is the probability that the resulting array is a minimum-oriented binary heap for n = 5 and 6?
Solution:1/15 and 1/36, respectively. Here is a nice discussion of the problem.


